题目内容
已知函数f（x）=ln（
-3x）+1，若f（lg（log210））=m，则f（lg（lg2））=（ ）
| 1+9x2 |
| A、-m | B、m | C、m+2 | D、2-m |
考点：函数的值
专题：函数的性质及应用
分析：设g（x）=ln（
-3x），则g（x）+g（-x）=ln[（
-3x）•（
-3x）]=ln1=0，从而f（x）+f（-x）=2，再由lg（log210）=-lg（lg2），得到f（lg（log210））+f（lg（lg2））=2，由此能求出f（lg（lg2））．
| 1+9x2 |
| 1+9x2 |
| 1+9x2 |
解答：
解：∵设g（x）=ln（
-3x），
∴g（-x）=ln（
+3x），
∴g（x）+g（-x）=ln[（
-3x）•（
-3x）]=ln1=0，
∴g（x）=ln（
-3x）是奇函数，
∴f（x）+f（-x）=2，
∵lg（log210）=-lg（lg2），
∴f（lg（log210））+f（lg（lg2））=2，
∴f（lg（lg2））=2-f（lg（log210））=2-m．
故选：D．
| 1+9x2 |
∴g（-x）=ln（
| 1+9x2 |
∴g（x）+g（-x）=ln[（
| 1+9x2 |
| 1+9x2 |
∴g（x）=ln（
| 1+9x2 |
∴f（x）+f（-x）=2，
∵lg（log210）=-lg（lg2），
∴f（lg（log210））+f（lg（lg2））=2，
∴f（lg（lg2））=2-f（lg（log210））=2-m．
故选：D．
点评：本题考查函数值的求法，是基础题，解题时要认真审题，注意函数的奇偶性和对数运算法则的合理运用．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
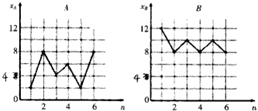如图，样本A和B分别来自两个不同的总体，它们的样本平均数分别为. |
| xA |
. |
| xB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在空间直角坐标系O-xyz中，已知A（2，0，0），B（2，2，0），C（0，2，0），D（1，1，
），若S1，S2，S3分别表示三棱锥D-ABC在xOy，yOz，zOx坐标平面上的正投影图形的面积，则（ ）
| 2 |
| A、S1=S2≠S3 |
| B、S2=S3≠S1 |
| C、S1=S3≠S2 |
| D、S1=S2=S3 |
若函数f（x）=
（x≠
）在定义域内恒有f[f（x）]=x，则m等于（ ）
| mx |
| 4x-3 |
| 3 |
| 4 |
| A、3 | ||
B、
| ||
C、-
| ||
| D、-3 |
双曲线2x2-y2=8的实轴长是（ ）
A、2
| ||
| B、2 | ||
C、4
| ||
| D、4 |