题目内容
已知
=3,
(Ⅰ)求tanθ的值;
(Ⅱ)sin2θ+sinθcosθ-cos2θ的值.
sin(π+θ)-2sin(
| ||||
cos(
|
(Ⅰ)求tanθ的值;
(Ⅱ)sin2θ+sinθcosθ-cos2θ的值.
考点:同角三角函数基本关系的运用,运用诱导公式化简求值
专题:计算题,三角函数的求值
分析:(Ⅰ)利用诱导公式化简后分子分母同除以cosθ即可求tanθ的值;
(Ⅱ)利用倍角公式和万能公式化简后代入(Ⅰ)的结论即可求sin2θ+sinθcosθ-cos2θ的值.
(Ⅱ)利用倍角公式和万能公式化简后代入(Ⅰ)的结论即可求sin2θ+sinθcosθ-cos2θ的值.
解答:
解:(Ⅰ)
=3,
⇒
=
=3,
⇒
=3,
⇒tanθ=-
.
(Ⅱ)sin2θ+sinθcosθ-cos2θ=
+
sin2θ-
=
sin2θ-cos2θ=
×
-
=
×
-
=-1.
sin(π+θ)-2sin(
| ||||
cos(
|
⇒
| -sinθ-2cosθ |
| -sinθ-cosθ |
| sinθ+2cosθ |
| sinθ+cosθ |
⇒
| tanθ+2 |
| tanθ+1 |
⇒tanθ=-
| 1 |
| 2 |
(Ⅱ)sin2θ+sinθcosθ-cos2θ=
| 1-cos2θ |
| 2 |
| 1 |
| 2 |
| 1+cos2θ |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2tanθ |
| 1+tan2θ |
| 1-tan2θ |
| 1+tan2θ |
| 1 |
| 2 |
| -1 | ||
1+
|
1-
| ||
1+
|
点评:本题主要考察了同角三角函数基本关系的运用,运用诱导公式化简求值,属于基本知识的考察.

练习册系列答案
相关题目
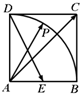 如图在边长为2的正方形ABCD中,E为边AB的中点,P为以A为圆心、AB为半径的圆弧上的任意一点,设向量
如图在边长为2的正方形ABCD中,E为边AB的中点,P为以A为圆心、AB为半径的圆弧上的任意一点,设向量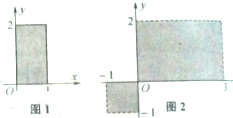 如图,图1中以阴影部分(含边界)的点为元素所组成的集合用描述法表示为{(x,y)|0≤x≤1,0≤y≤2},则图2中以阴影部分(不含外边界但包含坐标轴)的点为元素所组成的集合:
如图,图1中以阴影部分(含边界)的点为元素所组成的集合用描述法表示为{(x,y)|0≤x≤1,0≤y≤2},则图2中以阴影部分(不含外边界但包含坐标轴)的点为元素所组成的集合: