题目内容
已知a∈R,函数m(x)=x2,n(x)=aln(x+2).
(Ⅰ)令f(x)=
,若函数f(x)的图象上存在两点A、B满足OA⊥OB(O为坐标原点),且线段AB的中点在y轴上,求a的取值集合;
(Ⅱ)若函数g(x)=m(x)+n(x)存在两个极值点x1、x2,求g(x1)+g(x2)的取值范围.
(Ⅰ)令f(x)=
|
(Ⅱ)若函数g(x)=m(x)+n(x)存在两个极值点x1、x2,求g(x1)+g(x2)的取值范围.
考点:数量积判断两个平面向量的垂直关系,利用导数研究函数的极值
专题:综合题,导数的综合应用
分析:(Ⅰ)不妨设A(t,aln(t+2)),B(-t,t2),利用OA⊥OB,再分离参数,即可求a的取值集合;
(Ⅱ)函数g(x)=m(x)+n(x)存在两个极值点x1、x2,g′(x)=0,即2x2+4x+a=0在(-2,+∞)上存在两个不等的实根,可得0<a<2,x1+x2=-2,x1x2=
,表示出g(x1)+g(x2),确定其单调性,即可求g(x1)+g(x2)的取值范围.
(Ⅱ)函数g(x)=m(x)+n(x)存在两个极值点x1、x2,g′(x)=0,即2x2+4x+a=0在(-2,+∞)上存在两个不等的实根,可得0<a<2,x1+x2=-2,x1x2=
| a |
| 2 |
解答:
解:(Ⅰ)由题意,不妨设A(t,aln(t+2)),B(-t,t2)(t>0)
∴OA⊥OB,
∴-t2+at2ln(t+2)=0,
∴a=
,
∵ln(t+2)∈(ln2,+∞),
∴a的取值集合为(0,
);
(Ⅱ)g(x)=m(x)+n(x)=x2+aln(x+2),
∴g′(x)=
,
∵函数g(x)=m(x)+n(x)存在两个极值点x1、x2,
∴g′(x)=0,即2x2+4x+a=0在(-2,+∞)上存在两个不等的实根,
令p(x)=2x2+4x+a,
∴△=16-8a>0且p(-2)>0,
∴0<a<2,
∵x1+x2=-2,x1x2=
,
∴g(x1)+g(x2)=x12+aln(x1+2)+x22+aln(x2+2)
=(x1+x2)2-2x1x2+aln[x1x2+2(x1+x2)+4]
=aln
-a+4
令q(x)=xln
-x+4,x∈(0,2),
∴q′(x)=ln
<0,
∴q(x)在(0,2)上单调递减,
∴2<aln
-a+4<4
∴g(x1)+g(x2)的取值范围是(2,4).
∴OA⊥OB,
∴-t2+at2ln(t+2)=0,
∴a=
| 1 |
| ln(t+2) |
∵ln(t+2)∈(ln2,+∞),
∴a的取值集合为(0,
| 1 |
| ln2 |
(Ⅱ)g(x)=m(x)+n(x)=x2+aln(x+2),
∴g′(x)=
| 2x2+4x+a |
| x+2 |
∵函数g(x)=m(x)+n(x)存在两个极值点x1、x2,
∴g′(x)=0,即2x2+4x+a=0在(-2,+∞)上存在两个不等的实根,
令p(x)=2x2+4x+a,
∴△=16-8a>0且p(-2)>0,
∴0<a<2,
∵x1+x2=-2,x1x2=
| a |
| 2 |
∴g(x1)+g(x2)=x12+aln(x1+2)+x22+aln(x2+2)
=(x1+x2)2-2x1x2+aln[x1x2+2(x1+x2)+4]
=aln
| a |
| 2 |
令q(x)=xln
| x |
| 2 |
∴q′(x)=ln
| x |
| 2 |
∴q(x)在(0,2)上单调递减,
∴2<aln
| a |
| 2 |
∴g(x1)+g(x2)的取值范围是(2,4).
点评:本题考查导数知识的运用,考查韦达定理,考查函数的单调性与极值,考查学生的计算能力,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
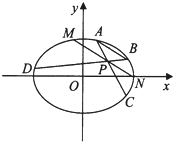 如图所示,离心率为
如图所示,离心率为