题目内容
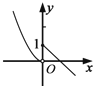
11.已知二次函数f(x)=ax2+bx+2(a,b∈R)(1)若此二次函数f(x)的最小值为f(-1)=1,求f(x)的解析式,并写出其单调区间;
(2)在(1)的条件下,f(x)>x+m在区间[1,3]上恒成立,试求m的范围.
分析 (1)利用二次函数f(x)的最小值为f(-1)=1,推出对称轴以及函数值,求解ab,得到函数的解析式.找出单调区间.
(2)通过分离变量,得到m的不等式,利用二次函数的最值求解即可.
解答 解:(1)由题意有f(-1)=a-b+2=1,
且-$\frac{b}{2a}$=-1,∴a=1,b=2.
∴f(x)=x2+2x+2,单调减区间为(-∞,-1),单调增区间为(-1,+∞).
(2)f(x)>x+m在区间[1,3]上恒成立,
即为x2+x+2>m在[1,3]上恒成立.
设g(x)=x2+x+2,x∈[1,3],
则g(x)在[1,3]上递增,∴g(x)min=g(1)=4.
∴m<4,即m的取值范围为(-∞,4).
点评 本题考查二次函数的性质的综合应用,函数的最值以及转化思想的应用,考查计算能力.

练习册系列答案
相关题目
1.若抛物线C1:y=$\frac{1}{4}$x2的焦点F到双曲线C2:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线的距离为$\frac{\sqrt{3}}{2}$,抛物线C1上的动点P到双曲线C2的一个焦点的距离与到直线y=-1的距离之和的最小时为$\sqrt{5}$,则双曲线C2的方程为( )
| A. | $\frac{{x}^{2}}{3}$-y2=1 | B. | x2-$\frac{{y}^{2}}{3}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{2}$=1 | D. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{3}$=1 |
2.某市进行一次高三教学质量抽样检测,考试后统计的所有考生的数学成绩服从正态分布.已知数学成绩平均分为90分,60分以下的人数占10%,则数学成绩在90分至120分之间的考生人数所占百分比约为40%.
19.在锐角△ABC中,内角A,B,C的对边分别为a,b,c,若sin2C-cos2C=$\frac{1}{2}$,则下列各式正确的是( )
| A. | a+b=2c | B. | a+b≤2c | C. | a+b<2c | D. | a+b≥2c |
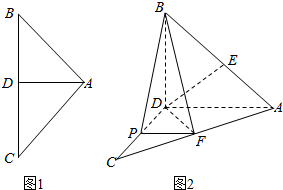 如图1,AD是等腰直角三角形ABC斜边上的高AB=4,沿AD把△ABC的两部分折成直二面角(如图2),P,E,F分别为CD,CA,BA的中点.求证:
如图1,AD是等腰直角三角形ABC斜边上的高AB=4,沿AD把△ABC的两部分折成直二面角(如图2),P,E,F分别为CD,CA,BA的中点.求证: