题目内容
16.已知{an}是首项为2且公差不为0的等差数列,若a1,a3,a6成等比数列,则{an}的前9项和等于( )| A. | 26 | B. | 30 | C. | 36 | D. | 40 |
分析 设公差为d,由已知得(2+2d)2=2(2+5d),且d≠0,解得d=$\frac{1}{2}$,由此能求出{an}的前9项和.
解答 解:设公差为d,
∵{an}是首项为2且公差不为0的等差数列,a1,a3,a6成等比数列,
∴(2+2d)2=2(2+5d),且d≠0,
解得d=$\frac{1}{2}$,
∴{an}的前9项和S9=$9×2+\frac{9×8}{2}×\frac{1}{2}$=36.
故选:C.
点评 本题考查等差数列的前9项和的求法,是基础题,解题时要认真审题,注意等差数列、等比数列的性质的合理运用.

练习册系列答案
相关题目
4. 为贯彻落实教育部6部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,培养拼搏意识和团队精神,普及足球知识和技能,市教体局决定举行春季校园足球联赛.为迎接此次联赛,甲中学选拔了20名学生组成集训队,现统计了这20名学生的身高,记录入如表:(设ξ为随机变量)
为贯彻落实教育部6部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,培养拼搏意识和团队精神,普及足球知识和技能,市教体局决定举行春季校园足球联赛.为迎接此次联赛,甲中学选拔了20名学生组成集训队,现统计了这20名学生的身高,记录入如表:(设ξ为随机变量)
(1)请计算这20名学生的身高的中位数、众数,并补充完成下面的茎叶图;
(2)身高为185cm和188cm的四名学生分别记为A,B,C,D,现从这四名学生选2名担任正副门将,请利用列举法列出所有可能情况,并求学生A入选门将的概率.
 为贯彻落实教育部6部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,培养拼搏意识和团队精神,普及足球知识和技能,市教体局决定举行春季校园足球联赛.为迎接此次联赛,甲中学选拔了20名学生组成集训队,现统计了这20名学生的身高,记录入如表:(设ξ为随机变量)
为贯彻落实教育部6部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,培养拼搏意识和团队精神,普及足球知识和技能,市教体局决定举行春季校园足球联赛.为迎接此次联赛,甲中学选拔了20名学生组成集训队,现统计了这20名学生的身高,记录入如表:(设ξ为随机变量)| 身高(cm) | 168 | 174 | 175 | 176 | 178 | 182 | 185 | 188 |
| 人数 | 1 | 2 | 4 | 3 | 5 | 1 | 3 | 1 |
(2)身高为185cm和188cm的四名学生分别记为A,B,C,D,现从这四名学生选2名担任正副门将,请利用列举法列出所有可能情况,并求学生A入选门将的概率.
11.下列函数中,既是奇函数又在区间(0,+∞)上单调递增的是( )
| A. | y=x3 | B. | y=lnx | C. | y=sinx | D. | y=2x |
1.已知实数x,y满足$\left\{\begin{array}{l}{y≥1}\\{y≤2x-1}\\{x+y≤m}\end{array}\right.$,如果目标函数z=y-x的最大值为1,则实数m等于( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
5.已知f(x)=$\frac{(a•{4}^{x}+2)cosx}{{2}^{x}}$为奇函数,则a的值为( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
6.在正项等比数列{an}中,a1008•a1009=$\frac{1}{100}$,则lga1+lga2+…+lga2016=( )
| A. | 2015 | B. | 2016 | C. | -2015 | D. | -2016 |
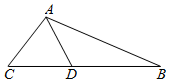 如图,在△ABC中,∠BAC=120°,AB=2,AC=1,D是BC边上的一点(包括端点),若$\overrightarrow{AD}$•$\overrightarrow{BC}$∈[m,n],则$\frac{n}{m-n}$的值为$-\frac{2}{7}$.
如图,在△ABC中,∠BAC=120°,AB=2,AC=1,D是BC边上的一点(包括端点),若$\overrightarrow{AD}$•$\overrightarrow{BC}$∈[m,n],则$\frac{n}{m-n}$的值为$-\frac{2}{7}$.