题目内容
8.过抛物线C:y2=2px(p>0)的焦点F的直线交抛物线于A,B两点,且A,B两点的纵坐标之积为-4.(1)求抛物线C的方程;
(2)已知点D的坐标为(4,0),若过D和B两点的直线交抛物线C的准线于P点,求证:直线AP与x轴交于一定点.
分析 (1)设A(x1,y1),B(x2,y2),设直线AB的方程为x=my+$\frac{p}{2}$,联立方程组,根据A,B两点的纵坐标之积为-4,即可求出p的值,
(2)表示出直线BD的方程可表示为,y=$\frac{{y}_{2}}{{x}_{2}-4}$(x-4)①,抛物线C的准线方程为,x=-1②,构成方程组,解得P的坐标,求出直线AP的斜率,得到直线AP的方程,求出交点坐标即可.
解答 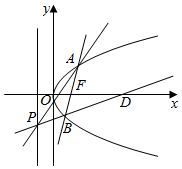 解:(1)设A(x1,y1),B(x2,y2),
解:(1)设A(x1,y1),B(x2,y2),
设直线AB的方程为x=my+$\frac{p}{2}$
与抛物线的方程联立$\left\{\begin{array}{l}{{y}^{2}=2px}\\{x=my+\frac{p}{2}}\end{array}\right.$,得y2-2mpy-p2=0,
∴y1•y2=-p2=-4,
解得p=±2,
∵p>0,
∴p=2,
∴直线BD的方程可表示为,y=$\frac{{y}_{2}}{{x}_{2}-4}$(x-4)①
∵抛物线C的准线方程为,x=-1②
由①,②联立方程组可求得P的坐标为(-1,-$\frac{5{y}_{2}}{{x}_{2}-4}$)
由(1)可得y1y2=-4,
∴P的坐标可化为(-1,$\frac{5{y}_{1}}{1-{y}_{1}^{2}}$),
∴kAP=$\frac{\frac{5{y}_{1}}{1-{y}_{1}^{2}}-{y}_{1}}{-1-{x}_{1}}$=$\frac{4{y}_{1}}{{y}_{1}^{2}-1}$,
∴直线AP的方程为y-y1=$\frac{4{y}_{1}}{{y}_{1}^{2}-1}$(x-x1),
令y=0,可得x=x1-$\frac{{y}_{1}^{2}-1}{4}$=$\frac{1}{4}{y}_{1}^{2}$-$\frac{{y}_{1}^{2}-1}{4}$=$\frac{1}{4}$
∴直线AP与x轴交于定点($\frac{1}{4}$,0).
点评 本题考查抛物线的方程,考查直线与抛物线的位置关系,考查直线过定点,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
19.在等比数列{an}中,a1=16,a6=2a5•a7,则a4=( )
| A. | 4 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
16.已知{an}是首项为2且公差不为0的等差数列,若a1,a3,a6成等比数列,则{an}的前9项和等于( )
| A. | 26 | B. | 30 | C. | 36 | D. | 40 |
20.已知α是三角形的最大内角,且cos2α=$\frac{1}{2}$,则$\frac{1-tanα}{1+tanα}$的值为( )
| A. | 2-$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 3-$\sqrt{3}$ | D. | 3+$\sqrt{3}$ |