��Ŀ����
4��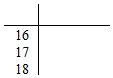 Ϊ�᳹��ʵ������6���š����ڼӿ췢չ������У�����ʵʩ�������ȫ�����������ѧ�������ʽ���ˮƽ������ƴ����ʶ���ŶӾ����ռ�����֪ʶ�ͼ��ܣ��н���־������д���У����������Ϊӭ�Ӵ˴�����������ѧѡ����20��ѧ����ɼ�ѵ�ӣ���ͳ������20��ѧ�������ߣ���¼������������Ϊ���������
Ϊ�᳹��ʵ������6���š����ڼӿ췢չ������У�����ʵʩ�������ȫ�����������ѧ�������ʽ���ˮƽ������ƴ����ʶ���ŶӾ����ռ�����֪ʶ�ͼ��ܣ��н���־������д���У����������Ϊӭ�Ӵ˴�����������ѧѡ����20��ѧ����ɼ�ѵ�ӣ���ͳ������20��ѧ�������ߣ���¼������������Ϊ���������| ���ߣ�cm�� | 168 | 174 | 175 | 176 | 178 | 182 | 185 | 188 |
| ���� | 1 | 2 | 4 | 3 | 5 | 1 | 3 | 1 |
��2������Ϊ185cm��188cm������ѧ���ֱ��ΪA��B��C��D���ִ�������ѧ��ѡ2�����������Ž����������оٷ��г����п������������ѧ��A��ѡ�Ž��ĸ��ʣ�
���� ��1����20��ѧ��������ͳ�Ʊ����������20��ѧ�������ߵ���λ��Ϊ����������������Ҷͼ��
��2�������оٷ���������Ž������п��������ѧ��A��ѡ���Ž����ж����ֿ��ܣ��ɴ������ѧ��A��ѡ���Ž��ĸ��ʣ�
��� �⣺��1����20��ѧ��������ͳ�Ʊ����õ���20��ѧ�������ߵ���λ��Ϊ177cm������Ϊ178cm��
��ҶͼΪ��
��2�������Ž������п������Ϊ��
��A��B������B��A������A��C������C��A������A��D������D��A������B��C������C��B������B��D������D��B������C��D������D��C����
��12�֣�
���У�ѧ��A��ѡ���Ž��ģ�A��B������A��C������A��D��3�ֿ��ܣ�
��ѧ��A��ѡ���Ž��ĸ���Ϊ$\frac{3}{12}=\frac{1}{4}$��
���� ���⿼����ʵ����ǻ����⣬����ʱҪ�������⣬ע���ʾ�����¼����ʼ��㹫ʽ�ĺ������ã�

��ϰ��ϵ�д�
 ѧҵ����һ��һ��ϵ�д�
ѧҵ����һ��һ��ϵ�д�
�����Ŀ
14����A1��A2�ֱ�Ϊ˫����$C��\frac{x^2}{a^2}-\frac{y^2}{b^2}=1��a��0��b��0��$�����Ҷ��㣬��˫�����ϴ��ڵ�Mʹ����ֱ��б��${k_{M{A_1}}}{k_{M{A_2}}}��2$����˫����C�������ʵ�ȡֵ��ΧΪ��������
| A�� | $��0��\sqrt{3}��$ | B�� | $��1��\sqrt{3}��$ | C�� | $��\sqrt{3}��+�ޣ�$ | D�� | ��0��3�� |
19���ڵȱ�����{an}�У�a1=16��a6=2a5•a7����a4=��������
| A�� | 4 | B�� | 2 | C�� | 1 | D�� | $\frac{1}{2}$ |
16����֪{an}������Ϊ2�ҹ��Ϊ0�ĵȲ����У���a1��a3��a6�ɵȱ����У���{an}��ǰ9��͵��ڣ�������
| A�� | 26 | B�� | 30 | C�� | 36 | D�� | 40 |
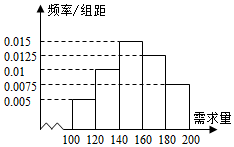 ��ѧ��С���ҵ��������ҵ������һ��С�Ϳ���������ũ��Ʒ�����������ջڣ�����1�����ѣ����������������500Ԫ������δ��������ʣ�࣬һ�ɰ�ÿ������300Ԫ���㣮���������г����飬�õ������ջ��г���������ֱ��ͼ����ͼ��ʾ�����������ջ�ļ��ڣ�С�������ũ����160�����ѣ���X����λ������100��X��200����ʾ���������ջڵ��г���������Y����λ��Ԫ����ʾ�����������۵�����
��ѧ��С���ҵ��������ҵ������һ��С�Ϳ���������ũ��Ʒ�����������ջڣ�����1�����ѣ����������������500Ԫ������δ��������ʣ�࣬һ�ɰ�ÿ������300Ԫ���㣮���������г����飬�õ������ջ��г���������ֱ��ͼ����ͼ��ʾ�����������ջ�ļ��ڣ�С�������ũ����160�����ѣ���X����λ������100��X��200����ʾ���������ջڵ��г���������Y����λ��Ԫ����ʾ�����������۵�����