题目内容
6.已知直线y=$\frac{3}{4}$x+b分圆x2+y2=4成的圆弧长之比为1:2,则实数b=±$\frac{5}{4}$.分析 由题意可得直线到圆心距离d=1,由点到直线的距离公式可得.
解答 解:∵直线y=$\frac{3}{4}$x+b分圆x2+y2=4成的圆弧长之比为1:2,
∴分成的圆心角分别为120°结合240°,
在120°的等腰直角三角形中可得的直线到圆心距离d=1,
化直线方程为一般式可得3x-4y+4b=0,
由距离公式可得$\frac{|4b|}{\sqrt{{3}^{2}+{4}^{2}}}$=1,解得b=±$\frac{5}{4}$
故答案为:±$\frac{5}{4}$
点评 本题考查直线和圆相交的性质,转化为点到直线的距离是解决问题的关键,属基础题.

练习册系列答案
相关题目
14.设A1,A2分别为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左右顶点,若双曲线上存在点M使得两直线斜率${k_{M{A_1}}}{k_{M{A_2}}}<2$,则双曲线C的离心率的取值范围为( )
| A. | $(0,\sqrt{3})$ | B. | $(1,\sqrt{3})$ | C. | $(\sqrt{3},+∞)$ | D. | (0,3) |
16.已知{an}是首项为2且公差不为0的等差数列,若a1,a3,a6成等比数列,则{an}的前9项和等于( )
| A. | 26 | B. | 30 | C. | 36 | D. | 40 |
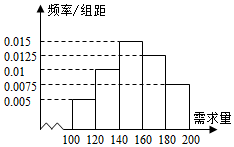 大学生小李毕业后自主创业,买了一辆小型卡车,运输农产品.在输葡萄收获季节,运输1车葡萄.当天批发完获利润500元,当天未批发或有剩余,一律按每车亏损300元计算.根据以往市场调查,得到葡萄收获季节市场需求量的直方图,如图所示,今年葡萄收获的季节,小李给当地农民定了160车葡萄,以X(单位:车,100≤X≤200)表示今年葡萄收获季节的市场需求量,Y(单位:元)表示今年葡萄销售的利润.
大学生小李毕业后自主创业,买了一辆小型卡车,运输农产品.在输葡萄收获季节,运输1车葡萄.当天批发完获利润500元,当天未批发或有剩余,一律按每车亏损300元计算.根据以往市场调查,得到葡萄收获季节市场需求量的直方图,如图所示,今年葡萄收获的季节,小李给当地农民定了160车葡萄,以X(单位:车,100≤X≤200)表示今年葡萄收获季节的市场需求量,Y(单位:元)表示今年葡萄销售的利润.