题目内容
已知椭圆C:
+
=1(a>b>0)上的点到椭圆右焦点F的最大距离为
+1,离心率e=
,直线l过点F与椭圆C交于A,B两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)C上是否存在点P,使得当l绕F转到某一位置时,有
=
+
成立?若存在,求出所有点P的坐标与l的方程;若不存在,说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| ||
| 3 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)C上是否存在点P,使得当l绕F转到某一位置时,有
| OP |
| OA |
| OB |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(I)由条件知
,由此能求出椭圆方程.
(Ⅱ)C上存在点P,使得当l绕F转到某一位置时,有
=
+
成立.由 (Ⅰ)知C的方程为2x2+3y2=6.设A(x1,y1),B(x2,y2),当l垂直于x轴时,C上不存在点P使
=
+
立.当l不垂直x轴时,设l的方程为y=k(x-1),将y=k(x-1)代入2x2+3y2=6,得:(2+3k2)x2-6k2x+3k2-6=0,由此能求出C上存在点P(
,±
),使
=
+
成立,此时l的方程为
x±y-
=0.
|
(Ⅱ)C上存在点P,使得当l绕F转到某一位置时,有
| OP |
| OA |
| OB |
| OP |
| OA |
| OB |
| 3 |
| 2 |
| ||
| 2 |
| OP |
| OA |
| OB |
| 2 |
| 2 |
解答:
解:(I)由条件知
,
解得
,
所以b2=a2-c2=2,
故椭圆方程为
+
=1.…(4分)
(Ⅱ)C上存在点P,使得当l绕F转到某一位置时,有
=
+
成立.
由 (Ⅰ)知C的方程为2x2+3y2=6.设A(x1,y1),B(x2,y2),
(ⅰ) 当l垂直于x轴时,由
+
=(2,0)知,
C上不存在点P使
=
+
成立. …(5分)
(ⅱ)当l不垂直x轴时,设l的方程为y=k(x-1),
将y=k(x-1)代入2x2+3y2=6,并化简,得:
(2+3k2)x2-6k2x+3k2-6=0,
于是x1+x2=
,x1x2=
,
C 上的点P使
=
+
成立的充要条件是P点坐标为(x1+x2,y1+y2),
设P(x0,y0),则
,…(7分)
所以x0=
,y0=
.因为P在椭圆上,
将x0,y0代入椭圆方程,得:3k4-4k2-4=0,
所以k2=2,k=±
,
当k=-
时,P(
,
),l的方程为
x+y-
=0.
当k=
时,P(
,-
),l的方程
x-y-
=0.…(9分)
综上,C上存在点P(
,±
),使
=
+
成立,
此时l的方程为
x±y-
=0.…(10分)
|
解得
|
所以b2=a2-c2=2,
故椭圆方程为
| x2 |
| 3 |
| y2 |
| 2 |
(Ⅱ)C上存在点P,使得当l绕F转到某一位置时,有
| OP |
| OA |
| OB |
由 (Ⅰ)知C的方程为2x2+3y2=6.设A(x1,y1),B(x2,y2),
(ⅰ) 当l垂直于x轴时,由
| OA |
| OB |
C上不存在点P使
| OP |
| OA |
| OB |
(ⅱ)当l不垂直x轴时,设l的方程为y=k(x-1),
将y=k(x-1)代入2x2+3y2=6,并化简,得:
(2+3k2)x2-6k2x+3k2-6=0,
于是x1+x2=
| 6k2 |
| 2+3k2 |
| 3k2-6 |
| 2+3k2 |
C 上的点P使
| OP |
| OA |
| OB |
设P(x0,y0),则
|
所以x0=
| 6k2 |
| 2+3k2 |
| -4k |
| 2+3k2 |
将x0,y0代入椭圆方程,得:3k4-4k2-4=0,
所以k2=2,k=±
| 2 |
当k=-
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| 2 |
| 2 |
当k=
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| 2 |
| 2 |
综上,C上存在点P(
| 3 |
| 2 |
| ||
| 2 |
| OP |
| OA |
| OB |
此时l的方程为
| 2 |
| 2 |
点评:本题考查椭圆方程的求法,考查满足条件的点的坐标和直线方程是否存在的判断与求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
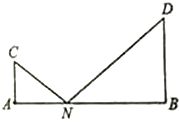 如图,C,D是两个小区的所在地,C,D到一条公路AB的垂直距离CA=1km,DB=2km,AB两端之间的距离为4km,某公交公司将在AB之间找一点N,在N处建造一个公交站台.
如图,C,D是两个小区的所在地,C,D到一条公路AB的垂直距离CA=1km,DB=2km,AB两端之间的距离为4km,某公交公司将在AB之间找一点N,在N处建造一个公交站台. 如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC=2,EA⊥EB.
如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC=2,EA⊥EB.