题目内容

已知函数f（x）=x2+ax+blnx（x＞0，实数a，b为常数），若a+b=-2，且b＜1，讨论f（x）的单调性．
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：求出导函数的根，讨论根在不在定义域内；若根在定义域内，讨论两根的大小；判断根左右两边导函数的符号，据单调性与导函数的关系求出单调性．
解答： 解：由于a+b=-2，则a=-2-b，
∴f（x）=x2-（2+b）x+blnx，
∴f′（x）=2x-（2+b）+
b
x

=
(2x-b)(x-1)
x
，
令f′（x）=0，解得：x=
b
2
，x=1，
∵b＜1，∴
b
2
＜
1
2
＜1，
①
b
2
≤0时，
∴f（x）在（0，1）递减，在（1，+∞）递增；
②0＜
b
2
＜
1
2
即0＜b＜1时，
∴函数f（x）的单调递增区间为（0，
b
2
），（1，+∞），
单调递减区间为（
b
2
，1）．
点评：本题考查利用导数研究函数的性质：求极值，求单调区间．考查分类讨论时注意分类的起点．
练习册系列答案
相关题目
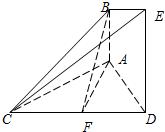如图，已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD=DE=2AB=2，F为CD的中点．
（1）求三棱锥D-BAC的体积；
（2）求证：AF∥平面BCE；
（3）求二面角B-CD-A的大小．
某发射装置上有一个特殊的按键，在发射装置的屏幕上显示正整数n时按下这个键，会等可能的将其替换为0～n-1中的任意一个数，反复按这个键使得最终显示0，我们把这一操作称为“还原”操作．
（Ⅰ）设初始值为15，求在“还原”操作中出现9的概率；
（Ⅱ）当初始值为4时，进行“还原”操作，记操作次数为ξ，求ξ的概率分布列与数学期望．
如图，直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直．AB∥CD，AB⊥BC，AB=2CD=2BC=2，EA⊥EB．
（Ⅰ）求直线EC与平面ABE所成角的正切值；
（Ⅱ）线段EA上是否存在点F，使EC∥平面FBD？存在请确定具体位置，不存在说明理由．
已知tan（π-α）=2，计算：
（1）
sinα+2cosα
sinα-2cosα

（2）
3sin2(π+α)-2cos2(π-α)+sin(2π-α)cos(π+α)
1+2sin2α+cos2α
．
已知二次函数f（x）=ax2+bx+c（a＞0）．
（Ⅰ）（i）若b=-2，且f（x）在（1，+∞）上为单调递增函数，求实数a的取值范围；
（ii）若b=-1，c=1，当x∈[0，1]时，|f（x）|的最大值为1，求实数a的取值范围；
（Ⅱ）若f（0）≥1，f（1）≥1，f（x）=0的有两个小于1的不等正根，求a的最小正整数值．
已知函数f（x）为定义域在（0，+∞）上的增函数，且满足f（2）=1，f（xy）=f（x）+f（y）
（1）求f（1），f（4）的值． 
（2）如果f（x）-f（x-3）＜2，求x的取值范围．
已知函数f（x）=
x2+2x，x＜0
lnx，x＞0
．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）当x≥1时，证明：曲线f（x）与g（x）=x-1仅有一个公共点；
（Ⅲ）设A（x1，f（x1）），B（x2，f（x2））（x1＜x2＜0）为曲线f（x）上的两点，且曲线f（x）在点A，B处的切线互相垂直，求x2-x1的最小值．
设数列{an}的通项公式为an=pn+q（n∈N*，p＞0）．数列{bn}定义如下：对于正整数m，bm是使得不等式an≥m成立的所有n中的最小值．
（Ⅰ）若p=
1
2
，q=-
1
3
，求b3；
（Ⅱ）若p=2，q=-1，求数列{bn}的前2m项和公式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网