题目内容
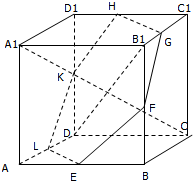如图所示正方体ABCD-A1B1C1D1中，E、F、G、H、K、L分别为AB、BB1、B1C1、C1D1、D1D、DA的中点，求DB1与平面EFGHKL所成角的余弦值．考点：直线与平面所成的角
专题：空间角
分析：设正方体ABCD-A1B1C1D1的棱长为1，由已知得cos＜
，
＞=
=-
，由
是平面EFGHKL的一个法向量，能求出DB1与平面EFGHKL所成角α的余弦值．
| A1C |
| DB1 |
| ||||
|
|
| 1 |
| 3 |
| A1C |
解答：
解：设正方体ABCD-A1B1C1D1的棱长为1，
∵
•
=（
+
）•（
+
）=-1，
|
|•|
|=（
）2=3，
∴cos＜
，
＞=
=-
，
∵
是平面EFGHKL的一个法向量，
∴DB1与平面EFGHKL所成角α的余弦值：
cosα=
=
．
∴DB1与平面EFGHKL所成角的余弦值为
．
∵
| A1C |
| DB1 |
| A1A |
| AC |
| DB |
| BB1 |
|
| A1C |
| DB1 |
| 3 |
∴cos＜
| A1C |
| DB1 |
| ||||
|
|
| 1 |
| 3 |
∵
| A1C |
∴DB1与平面EFGHKL所成角α的余弦值：
cosα=
1-(-
|
2
| ||
| 3 |
∴DB1与平面EFGHKL所成角的余弦值为
2
| ||
| 3 |
点评：本题考查直线与平面所成角的余弦值的求法，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
如果复数（m2-3m）+（m2-5m+6）i是纯虚数，则实数m的值为（ ）
| A、0 | B、2 | C、0或3 | D、2或3 |
设i是虚数单位，复数Z=
，则
=（ ）
| 2 |
| 1+i |
| Z |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |