题目内容
将(x+y+z)9展开之后再合并同类项,所得的多项式的项数是 .
考点:二项式定理的应用
专题:归纳法
分析:根据题意,(x+y+z)9展开后合并同类项,所得多项式的每一项都是由k•xn1•yn2•zn3组成,且n1+n2+n3=9,ni≥0,ni∈N;求出上式有多少组解即可.
解答:
解:(x+y+z)9展开后合并同类项,所得多项式的每一项都是由k•xn1•yn2•zn3组成,其中k>0;
且n1+n2+n3=9,ni≥0,ni∈N;
∴上式共有
=
=55组解.
故答案为:55.
且n1+n2+n3=9,ni≥0,ni∈N;
∴上式共有
| C | 3-1 9+3-1 |
| C | 2 11 |
故答案为:55.
点评:本题考查了归纳猜想与二项式定理的应用问题,解题时应通过简单的例子归纳分析,总结得出正确的结论,是易错题.

练习册系列答案
相关题目
把正整数排列成如图甲的三角形数阵,然后擦去第偶数行的奇数和第奇数行中的偶数,得到如图乙的三角数阵,再把图乙中的数按从小到大的顺序排成一列,得到数列{an},若an=2013,则n的值为( )


| A、1029 | B、1031 |
| C、1033 | D、1035 |
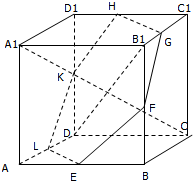 如图所示正方体ABCD-A1B1C1D1中,E、F、G、H、K、L分别为AB、BB1、B1C1、C1D1、D1D、DA的中点,求DB1与平面EFGHKL所成角的余弦值.
如图所示正方体ABCD-A1B1C1D1中,E、F、G、H、K、L分别为AB、BB1、B1C1、C1D1、D1D、DA的中点,求DB1与平面EFGHKL所成角的余弦值.