题目内容
已知长方形ABCD，AB=3，BC=2，E为BC中点，P为AB上一点，试利用向量知识判定点P在什么位置时，∠PED=45°．
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：把角∠PED看成向量
与
的夹角，以
、
为基底，用基底表示
与
，再代入两向量的夹角公式即可解出．
| EP |
| ED |
| BA |
| BC |
| EP |
| ED |
解答：
解：设
=
、
=
，则
、
为表示平面的一组基底，
且|
|=3，|
|=2，
⊥
，∠PED为向量
与
的夹角，
又
∥
，可设
=t
，∴
=
-
=t
-
，
而
=
-
=
+
-
=
+
=
+
．
∴
•
=（t
-
）•（
+
）=t
2-
2=9t-1，
|
|=
=
，|
|=
=
，
∴cos∠PED=
=
=
，
解得t=
、t=-
（舍）
∴点P在AB的一个3等分点时，∠PED=45°．
| BA |
| a |
| BC |
| b |
| a |
| b |
且|
| a |
| b |
| a |
| b |
| EP |
| ED |
又
| BP |
| BA |
| BP |
| a |
| EP |
| BP |
| BE |
| a |
| 1 |
| 2 |
| b |
而
| ED |
| BD |
| BE |
| BC |
| BA |
| 1 |
| 2 |
| BC |
| BA |
| 1 |
| 2 |
| BC |
| a |
| 1 |
| 2 |
| b |
∴
| EP |
| ED |
| a |
| 1 |
| 2 |
| b |
| a |
| 1 |
| 2 |
| b |
| a |
| 1 |
| 4 |
| b |
|
| EP |
(t
|
| 9t2+1 |
| ED |
(
|
| 10 |
∴cos∠PED=
| ||||
|
|
| 9t-1 | ||||
|
| ||
| 2 |
解得t=
| 2 |
| 3 |
| 1 |
| 6 |
∴点P在AB的一个3等分点时，∠PED=45°．
点评：本题考查平面向量知识的综合运用，其中要应用平面向量基本定理去解题时，要用基底向量正确表示其它向量．
练习册系列答案
相关题目
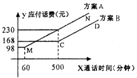电信局为满足不同客户的需要，设有A、B两种优惠方案，这两种方案应付话费（元）与通话时间（分钟）之间的关系如图（MN∥CD），若通话时间为500分钟，则应选择哪种方案更优惠（ ）| A、方案A | B、方案B |
| C、两种方案一样优惠 | D、不能确定 |
若数列{an}为等差数列，ap=q，aq=p（p≠q），则ap+q=（ ）
| A、p+q | ||
| B、0 | ||
| C、-（p+q） | ||
D、
|
在空间坐标中，O为坐标原点，A（1，2，3），则|OA|等于（ ）
A、
| ||
B、
| ||
C、2
| ||
D、
|
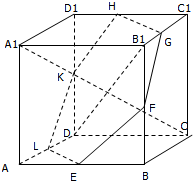如图所示正方体ABCD-A1B1C1D1中，E、F、G、H、K、L分别为AB、BB1、B1C1、C1D1、D1D、DA的中点，求DB1与平面EFGHKL所成角的余弦值．已知函数f（x）=ax2+bx+c（a＞0），且f（-1）=f（3），则（ ）
A、f（-3）＜c＜f（
| ||
B、f（
| ||
C、f（
| ||
D、c＜f（
|
下列各式中，正确的是（ ）
A、2
| ||
B、2
| ||
C、{2
| ||
D、{2
|