题目内容
用数学归纳法证明:32n+2-8n-9(n∈N)能被64整除.
考点:数学归纳法
专题:证明题,点列、递归数列与数学归纳法
分析:利用数学归纳法来证明,当n=1时,命题成立,再假设当n=k时,f(k)=32k+2-8k-9能够被64整除,证明当n=k+1时,命题也成立.
解答:
证明:(1)当n=1时,f(1)═34-8-9=64能被64整除,命题成立.
(2)假设当n=k时,f(k)=32k+2-8k-9能够被64整除.
当n=k+1时,f(k+1)=32k+4-8(k+1)-9=9[32k+2-8k-9]+64k+64=9[32k+2-8k-9]+64(k+1)
∵f(k)=32k+2-8k-9能够被64整除,
∴f(k+1)=9[32k+2-8k-9]+64(k+1)能够被64整除.
即当n=k+1时,命题也成立.
由(1)(2)可知,f(n)=32n+2-8n-9(n∈N*)能被64整除,即f(n)=32n+2-8n-9是64的倍数.
(2)假设当n=k时,f(k)=32k+2-8k-9能够被64整除.
当n=k+1时,f(k+1)=32k+4-8(k+1)-9=9[32k+2-8k-9]+64k+64=9[32k+2-8k-9]+64(k+1)
∵f(k)=32k+2-8k-9能够被64整除,
∴f(k+1)=9[32k+2-8k-9]+64(k+1)能够被64整除.
即当n=k+1时,命题也成立.
由(1)(2)可知,f(n)=32n+2-8n-9(n∈N*)能被64整除,即f(n)=32n+2-8n-9是64的倍数.
点评:本题考查数学归纳法的运用,解题的关键正确运用数学归纳法的证题步骤,属于中档题.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
已知f(x)是R上的偶函数,对任意的x1,x2∈[0,+∞)(x1≠x2),有
<0,则f(-2),f(-π),f(3)的大小关系是( )
| f(x2)-f(x1) |
| x2-x1 |
| A、f(-π)>f(-2)>f(3) |
| B、f(3)>f(-π)>f(-2) |
| C、f(-2)>f(3)>f(-π) |
| D、f(-π)>f(3)>f(-2) |
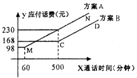 电信局为满足不同客户的需要,设有A、B两种优惠方案,这两种方案应付话费(元)与通话时间(分钟)之间的关系如图(MN∥CD),若通话时间为500分钟,则应选择哪种方案更优惠( )
电信局为满足不同客户的需要,设有A、B两种优惠方案,这两种方案应付话费(元)与通话时间(分钟)之间的关系如图(MN∥CD),若通话时间为500分钟,则应选择哪种方案更优惠( )| A、方案A | B、方案B |
| C、两种方案一样优惠 | D、不能确定 |
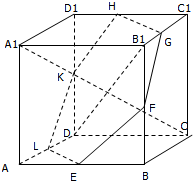 如图所示正方体ABCD-A1B1C1D1中,E、F、G、H、K、L分别为AB、BB1、B1C1、C1D1、D1D、DA的中点,求DB1与平面EFGHKL所成角的余弦值.
如图所示正方体ABCD-A1B1C1D1中,E、F、G、H、K、L分别为AB、BB1、B1C1、C1D1、D1D、DA的中点,求DB1与平面EFGHKL所成角的余弦值.