题目内容
已知函数f（x）满足f（x+2）=f（x），f（2+x）=f（2-x）且x∈[2，3]时，f（x）=（x-2）2，求f（x）在[4，6]上的解析式．
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：通过已知条件知道，f（x）的周期为2，f（x）图象关于x=2对称，x∈[2，3]上的图象关于x=2对称，所以在区间[1，2]上的解析式也是f（x）=（x-2）2，即f（x）在[1，3]上的解析式为：f（x）=f（x-2）2．经过一个周期，得到f（x）在[4，5]上的图象，解析式为f（x）=（x-4）2，再经过一个周期得到f（x）在（5，6]上的图象，解析式为f（x）=（x-6）2，合在一起便得到f（x）在[4，6]上的解析式．
解答：
解：f（2+x）=f（2-x）得出f（x）图象关于x=2对称；
x∈[2，3]上的f（x）=（x-2）2关于x=2对称，∴在[1，2]上的函数f（x）解析式也是f（x）=（x-2）2；
即在[1，3]上函数f（x）=（x-2）2；
由f（x+2）=f（x）知道f（x）的周期为2，而[1，3]正好是f（x）的一个周期，向右平移一个周期，再平移一个周期的图象如下：
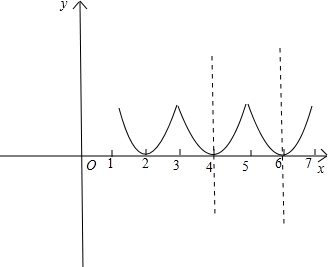
由图可看出[4，5]上的解析式f（x）=（x-2-2）2=（x-4）2，（5，6]上的解析式为，f（x）=（x-2-2-2）2=（x-6）2；
即f（x）在[4，6]上的解析式为：f(x)=
．
x∈[2，3]上的f（x）=（x-2）2关于x=2对称，∴在[1，2]上的函数f（x）解析式也是f（x）=（x-2）2；
即在[1，3]上函数f（x）=（x-2）2；
由f（x+2）=f（x）知道f（x）的周期为2，而[1，3]正好是f（x）的一个周期，向右平移一个周期，再平移一个周期的图象如下：
由图可看出[4，5]上的解析式f（x）=（x-2-2）2=（x-4）2，（5，6]上的解析式为，f（x）=（x-2-2-2）2=（x-6）2；
即f（x）在[4，6]上的解析式为：f(x)=
|
点评：考查函数周期的概念，图象关于某直线对称的表示形式，二次函数图象及其对称性．
练习册系列答案
相关题目
已知f（x）是R上的偶函数，对任意的x1，x2∈[0，+∞）（x1≠x2），有
＜0，则f（-2），f（-π），f（3）的大小关系是（ ）
| f(x2)-f(x1) |
| x2-x1 |
| A、f（-π）＞f（-2）＞f（3） |
| B、f（3）＞f（-π）＞f（-2） |
| C、f（-2）＞f（3）＞f（-π） |
| D、f（-π）＞f（3）＞f（-2） |
在空间坐标中，O为坐标原点，A（1，2，3），则|OA|等于（ ）
A、
| ||
B、
| ||
C、2
| ||
D、
|
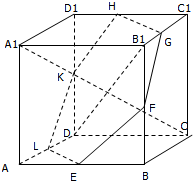如图所示正方体ABCD-A1B1C1D1中，E、F、G、H、K、L分别为AB、BB1、B1C1、C1D1、D1D、DA的中点，求DB1与平面EFGHKL所成角的余弦值．