Question

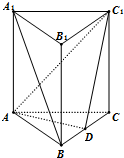直三棱柱ABC-A₁B₁C₁中，AB⊥AC，AB=AC=2，AA₁=4，D为BC中点，
（1）求证：A₁B∥面C₁AD；
（2）求异面直线A₁B与C₁D所成角的余弦值；
（3）求平面ADC₁与平面ABA₁所成锐二面角的正弦值．

Answer 1

考点：二面角的平面角及求法,异面直线及其所成的角,直线与平面平行的判定

专题：空间位置关系与距离,空间角

分析：（1）以A为原点，AB为x轴，AC为y轴，AA₁为z轴，建立空间直角坐标系，利用向量法能证明A₁B∥面C₁AD．
（2）由

A1B

=（2，0，-4），

C1D

=（1，-1，-4），能求出直线A₁B与C₁D所成角的余弦值．
（3）求出平面ADC₁的法向量和平面ABA₁的法向量，由此能求出面ADC₁与面ABA₁所成锐二面角的正弦值．

解答： （1）证明：以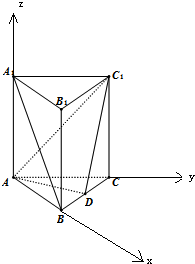A为原点，AB为x轴，AC为y轴，AA₁为z轴，
建立空间直角坐标系，
A₁（0，0，4），B（2，0，0），A（0，0，0），C₁（0，2，4），
C（0，2，0），D（1，1，0），

A1B

=（2，0，-4），

AD

=（1，1，0），

AC1

=（0，2，4），
设平面C₁AD的法向量

n

=（x，y，z），
则

n • AD =x+y=0 n • AC1 =2y+4z=0

，
取y=-2，得

n

=（2，-2，1），
∵

A1B

•

n

=4+0-4=0，A₁B不包含于平面C₁AD，
∴A₁B∥面C₁AD．
（2）解：∵

A1B

=（2，0，-4），

C1D

=（1，-1，-4），
∴cos＜

A1B

，

C1D

＞=

2+0+16

4+16 × 1+1+16

=

3 10

10

，
∴直线A₁B与C₁D所成角的余弦值为

3 10

10

．
（3）∵平面ADC₁的法向量

n

=(2，-2，1)，
平面ABA₁的法向量

m

=（0，1，0），
∴|cos＜

n

，

m

＞|=|

-2

9

|=

2

3

，
设平面ADC₁与平面ABA₁所成锐二面角为θ，
则cosθ=

2

3

，sinθ=

1- 4 9

=

5

3

，
∴平面ADC₁与平面ABA₁所成锐二面角的正弦值为

5

3

．

点评：本题考查直线与平面垂直的证明，考查直线与直线所成角的余弦值的求法，考查平面与平面所成的锐二面角的求法，解题时要注意向量法的合理运用．