题目内容
已知数列{an}的前n项和Sn=n2,{bn}为等比数列,且a1=b1,b1(a2-a1)=b2,
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)设cn=
,求数列{cn}的前n项和Tn.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)设cn=
| an |
| 2bn |
考点:数列的求和,数列递推式
专题:综合题,等差数列与等比数列
分析:(Ⅰ)当n=1时,a1=S1=1,a2=S2-S1得到an的通项公式,得到即可;因为b1=a1=1,并且b1(a2-a1)=b2即可解出q,然后得到通项;
(Ⅱ)利用错位相减法,可求数列{cn}的前n项和Tn.
(Ⅱ)利用错位相减法,可求数列{cn}的前n项和Tn.
解答:
解:(Ⅰ)由Sn=n2得数列{an}是等差数列,设公差为d,
∵a1=S1=1,a2=S2-S1=3,
∴d=2,
∴an=2n-1,
∵b1=1,b1(a2-a1)=b2=2
∴bn=2n-1;
(Ⅱ)cn=
=
=
,
∴Tn=
+
+…+
,
Tn=
+
+…+
上式相减,整理得:Tn=3-
.
∵a1=S1=1,a2=S2-S1=3,
∴d=2,
∴an=2n-1,
∵b1=1,b1(a2-a1)=b2=2
∴bn=2n-1;
(Ⅱ)cn=
| an |
| 2bn |
| 2n-1 |
| 2×2n-1 |
| 2n-1 |
| 2n |
∴Tn=
| 1 |
| 2 |
| 3 |
| 22 |
| 2n-1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 3 |
| 23 |
| 2n-1 |
| 2n+1 |
上式相减,整理得:Tn=3-
| 2n+3 |
| 2n |
点评:本题考查等差数列、等比数列的通项公式,考查错位相减法的运用,属于中档题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
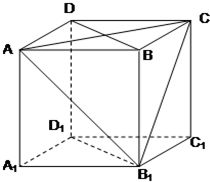 在正方体ABCD-A1B1C1D1中,
在正方体ABCD-A1B1C1D1中,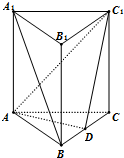 直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=2,AA1=4,D为BC中点,
直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=2,AA1=4,D为BC中点,