题目内容
已知|
|=1，|
|=2
（1）若
∥
，求
•
的值；
（2）若
，
不共线，且对?t∈R，|t
+
|≥|
-
|恒成立，求
，
的夹角θ．
| a |
| b |
（1）若
| a |
| b |
| a |
| b |
（2）若
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（1）由于
∥
，可得＜
，
＞=0或π；
（2）由|t
+
|≥|
-
|，利用数量积的运算性质可得：
≥
，化为t2+4tcosθ+4cosθ-1≥0，由于
，
不共线，且对?t∈R，|t
+
|≥|
-
|恒成立，可得△≤0，解出即可．
| a |
| b |
| a |
| b |
（2）由|t
| a |
| b |
| a |
| b |
t2
|
|
| a |
| b |
| a |
| b |
| a |
| b |
解答：
解：（1）∵
∥
，
∴
•
=|
||
|cos＜
，
＞=1×2cos＜
，
＞=±2；
（2）由|t
+
|≥|
-
|可得：
≥
，
化为t2+4tcosθ+4cosθ-1≥0，
∵
，
不共线，且对?t∈R，|t
+
|≥|
-
|恒成立，
∴△=16cos2θ-4（4cosθ-1）≤0，
化为（2cosθ-1）2≤0，
∴cosθ=
，
∵θ∈[0，π]，∴θ=
．
| a |
| b |
∴
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
（2）由|t
| a |
| b |
| a |
| b |
t2
|
|
化为t2+4tcosθ+4cosθ-1≥0，
∵
| a |
| b |
| a |
| b |
| a |
| b |
∴△=16cos2θ-4（4cosθ-1）≤0，
化为（2cosθ-1）2≤0，
∴cosθ=
| 1 |
| 2 |
∵θ∈[0，π]，∴θ=
| π |
| 3 |
点评：本题考查了向量共线定理、数量积运算性质、一元二次不等式的解集与判别式的关系，考查了推理能力和计算能力，属于中档题．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
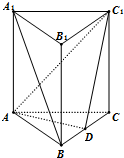直三棱柱ABC-A1B1C1中，AB⊥AC，AB=AC=2，AA1=4，D为BC中点，
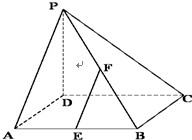如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD=DC，E，F分别是AB，PB的中点．