题目内容
若0＜a＜b＜1，比较a+b，2
，2ab的大小，并按从小到大的顺序排列．
| ab |
考点：不等式比较大小
专题：不等式的解法及应用
分析：0＜a＜b＜1，利用基本不等式可得：a+b＞2
，又0＜ab＜1．可得ab-a2b2=ab（1-ab）＞0．于是
＞ab．即可得出．
| ab |
| ab |
解答：
解：∵0＜a＜b＜1，
∴a+b＞2
，0＜ab＜1．
∵ab-a2b2=ab（1-ab）＞0．
∴
＞ab，即2
＞2ab．
∴2ab＜2
＜a+b．
∴a+b＞2
| ab |
∵ab-a2b2=ab（1-ab）＞0．
∴
| ab |
| ab |
∴2ab＜2
| ab |
点评：本题考查了基本不等式的性质、作差法比较两个数的大小，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
下列命题是真命题的是（ ）
| A、若ac＞bc，则a＞b | ||||
| B、若a＞b，c＞d，则ac＞bd | ||||
C、若a＞b，则
| ||||
| D、若c＞d，a-c＞b-d，则a＞b |
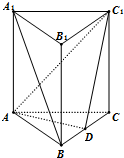直三棱柱ABC-A1B1C1中，AB⊥AC，AB=AC=2，AA1=4，D为BC中点，