题目内容
已知函数f(x)=4x+2x+1,x∈[-1,1],求f(x)的最大、最小值.
考点:函数的最值及其几何意义
专题:计算题,函数的性质及应用
分析:化简函数,设2x=t,代换后分析二次函数的最大值与最小值.
解答:
解:y=f(x)=4x+2x+1═4x+2•2x,
设2x=t,由x∈[-1,1],得t∈[
,2],
∴原式可化为y=t2+2t,t∈[
,2].
∵y关于t的函数是二次函数,且在[-1,+∞)上是增函数,
∴在[
,2]上也是增函数.
故当t=
,即x=-1时,y取到最小值
,
当t=2,即x=1时y取到最大值8.
设2x=t,由x∈[-1,1],得t∈[
| 1 |
| 2 |
∴原式可化为y=t2+2t,t∈[
| 1 |
| 2 |
∵y关于t的函数是二次函数,且在[-1,+∞)上是增函数,
∴在[
| 1 |
| 2 |
故当t=
| 1 |
| 2 |
| 5 |
| 4 |
当t=2,即x=1时y取到最大值8.
点评:本题考查了换元的方法应用及函数的单调性与最值.

练习册系列答案
相关题目
 某研究机构对高三学生的记忆力x和判断力y进行统计分析,所得数据如表所示:
某研究机构对高三学生的记忆力x和判断力y进行统计分析,所得数据如表所示:

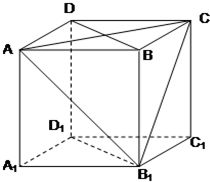 在正方体ABCD-A1B1C1D1中,
在正方体ABCD-A1B1C1D1中,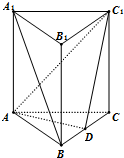 直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=2,AA1=4,D为BC中点,
直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=2,AA1=4,D为BC中点,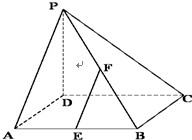 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.