题目内容
已知函数f（x）=loga（x+1）-loga（1-x），a＞0且a≠1．
（1）求f（x）的定义域；
（2）判断f（x）的奇偶性并予以证明．
（1）求f（x）的定义域；
（2）判断f（x）的奇偶性并予以证明．
考点：函数奇偶性的判断,函数的定义域及其求法
专题：函数的性质及应用
分析：（1）使函数各部分都有意义的自变量的范围，即列出不等式组
，解此不等式组求出x范围就是函数的定义域；
（2）根据函数奇偶性的定义进行证明即可．
|
（2）根据函数奇偶性的定义进行证明即可．
解答：
解：（1）由题得，使解析式有意义的x范围是使不等式组
成立的x范围，解得-1＜x＜1，
所以函数f（x）的定义域为{x|-1＜x＜1}．
（2）函数f（x）为奇函数，
证明：由（1）知函数f（x）的定义域关于原点对称，
且f（-x）=loga（-x+1）-loga（1+x）=-loga（1+x）+loga（1-x）=-[loga（1+x）-loga（1-x）]=-f（x）
所以函数f（x）为奇函数．
|
所以函数f（x）的定义域为{x|-1＜x＜1}．
（2）函数f（x）为奇函数，
证明：由（1）知函数f（x）的定义域关于原点对称，
且f（-x）=loga（-x+1）-loga（1+x）=-loga（1+x）+loga（1-x）=-[loga（1+x）-loga（1-x）]=-f（x）
所以函数f（x）为奇函数．
点评：本题主要考查函数定义域的求法，以及函数奇偶性的判断，利用函数奇偶性的定义是解决本题的关键
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
某研究机构对高三学生的记忆力x和判断力y进行统计分析，所得数据如表所示：
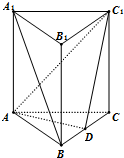直三棱柱ABC-A1B1C1中，AB⊥AC，AB=AC=2，AA1=4，D为BC中点，