题目内容
已知数列{an}中,a1=2,其前n项和Sn满足Sn+1-Sn=2n+1(n∈N+).
(1)求数列{an}的通项公式an以及前n和Sn;
(2)令bn=2log2an+1.求数列{
}的前n项和Tn.
(1)求数列{an}的通项公式an以及前n和Sn;
(2)令bn=2log2an+1.求数列{
| 1 |
| bn•bn+1 |
考点:数列的求和
专题:综合题,等差数列与等比数列
分析:(1)利用Sn+1-Sn=2n+1求数列{an}的通项公式an,利用等比数列的前n项和公式求前n和Sn;
(2)利用裂项法,求数列{
}的前n项和Tn.
(2)利用裂项法,求数列{
| 1 |
| bn•bn+1 |
解答:
解:(1)∵Sn+1-Sn=2n+1,
∴an+1=2n+1,
∴an=2n,
∴Sn=
=2n+1-2;
(2)bn=2log2an+1=2n+1,
∴
=
(
-
),
∴Tn=
(
-
+
-
+…+
-
)=
(
-
)=
.
∴an+1=2n+1,
∴an=2n,
∴Sn=
| 2(1-2n) |
| 1-2 |
(2)bn=2log2an+1=2n+1,
∴
| 1 |
| bn•bn+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 2n+3 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2n+1 |
| 1 |
| 2n+3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n+3 |
| n |
| 6n+9 |
点评:本题考查等比数列的通项与求和,考查裂项法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 某研究机构对高三学生的记忆力x和判断力y进行统计分析,所得数据如表所示:
某研究机构对高三学生的记忆力x和判断力y进行统计分析,所得数据如表所示:

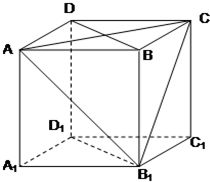 在正方体ABCD-A1B1C1D1中,
在正方体ABCD-A1B1C1D1中,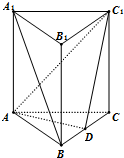 直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=2,AA1=4,D为BC中点,
直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=2,AA1=4,D为BC中点,