题目内容
5.焦点为F的抛物线C:y2=8x的准线与x轴交于点A,点M在抛物线C上,则当$\frac{{|{MA}|}}{{|{MF}|}}$取得最大值时,直线MA的方程为( )| A. | y=x+2或y=-x-2 | B. | y=x+2 | C. | y=2x+2或y=-2x+2 | D. | y=-2x+2 |
分析 由题意可知则当$\frac{{|{MA}|}}{{|{MF}|}}$取得最大值,则∠MAF必须取得最大值,此时AM与抛物线相切,设直线l的方程,代入抛物线方程,由△=0,考虑求得MA的方程.
解答  解:过M做MP与准线垂足,垂足为P,则$\frac{{|{MA}|}}{{|{MF}|}}$=$\frac{丨MA丨}{丨MP丨}$=$\frac{1}{cos∠AMP}$=$\frac{1}{cos∠MAF}$,则当$\frac{{|{MA}|}}{{|{MF}|}}$取得最大值,
解:过M做MP与准线垂足,垂足为P,则$\frac{{|{MA}|}}{{|{MF}|}}$=$\frac{丨MA丨}{丨MP丨}$=$\frac{1}{cos∠AMP}$=$\frac{1}{cos∠MAF}$,则当$\frac{{|{MA}|}}{{|{MF}|}}$取得最大值,
则∠MAF必须取得最大值,此时AM与抛物线相切,
设切线方程为y=k(x+2),则$\left\{\begin{array}{l}{y=k(x+2)}\\{{y}^{2}=8x}\end{array}\right.$,ky2-8y+16k=0,
△=64-64k2=0,k2=1,则k±1,
则直线方程y=x+2或y=-x-2,
故选:A.
点评 本题考查抛物线的性质,直线与抛物线的位置关系,考查数形结合思想,属于中档题.

练习册系列答案
相关题目
16.已知集合A={x|x2-6x+5≤0},B={x||2x-3|<1},则A∩B=( )
| A. | (1,2) | B. | [1,2) | C. | (2,5] | D. | [2,5] |
13.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )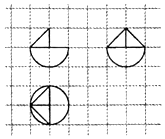

| A. | $\frac{2π+1}{3}$ | B. | $\frac{4π+1}{3}$ | C. | $\frac{2π+3}{3}$ | D. | $\frac{2π+2}{3}$ |
20.已知集合$A=\left\{{\left.{x∈Z}\right|\frac{4-x}{x+2}≥0}\right\}$,$B=\left\{{\left.x\right|\frac{1}{4}≤{2^x}≤4}\right\}$,则A∩B=( )
| A. | {x|-1≤x≤2} | B. | {-1,0,1,2} | C. | {-2,-1,0,1,2} | D. | {0,1,2} |
17.已知双曲线C1:$\frac{x^2}{4}-\frac{y^2}{3}=1$与双曲线C2:$\frac{x^2}{4}-\frac{y^2}{3}=-1$,给出下列说法,其中错误的是( )
| A. | 它们的焦距相等 | B. | 它们的焦点在同一个圆上 | ||
| C. | 它们的渐近线方程相同 | D. | 它们的离心率相等 |
15.过点(1,0)且与直线x+3y-5=0平行的直线方程是( )
| A. | x+3y+1=0 | B. | x+3y-1=0 | C. | 3x-y-3=0 | D. | 3x+y-3=0 |
 如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C为菱形,B1C⊥AC1.
如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C为菱形,B1C⊥AC1.