题目内容
11.在三棱锥P-ABC中,PB⊥AC,PB=9,AC=6,G为△PAC的重心,过点G作三棱锥的一个截面,使截面平行于直线PB和AC,则截面的面积为12.分析 作出截面四边形,利用相似比得出截面边长,证明截面为矩形,从而可得截面面积.
解答 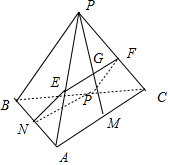 解:过G作EF∥AC,交PA,PC于E,F两点,
解:过G作EF∥AC,交PA,PC于E,F两点,
分布过E,F作PB的平行线交AB、BC于N,P,连结NP,
则四边形EFPN为所求截面.
∵EF∥AC,EN∥PB,∴EF⊥EN,
延长PG交AC于M,则$\frac{PG}{PM}=\frac{2}{3}$,∴EF=4,
∵$\frac{EN}{PB}=\frac{AE}{AP}$=$\frac{1}{3}$,∴NE=3,
同理可得FP=3,NP=4,
∴四边形EFPN是矩形,
∴S矩形EFPN=3×4=12.
故答案为:12.
点评 本题考查了棱锥的结构特征,属于中档题.

练习册系列答案
相关题目
19.在数列{an}中,a1=1,an=$\frac{n-1}{n}$an-1(n≥2),则通项公式an等于( )
| A. | $\frac{n-1}{n}$ | B. | $\frac{1}{n}$ | C. | $\frac{n}{n-1}$ | D. | $\frac{n+1}{n}$ |
16.已知集合A={x|x2-6x+5≤0},B={x||2x-3|<1},则A∩B=( )
| A. | (1,2) | B. | [1,2) | C. | (2,5] | D. | [2,5] |
3.设集合A={-1,1,2,3},集合B={-2,-1,0,1}则A∩B=( )
| A. | {-2,-1,1,2} | B. | {-1,1} | C. | {2} | D. | {1} |
20.已知集合$A=\left\{{\left.{x∈Z}\right|\frac{4-x}{x+2}≥0}\right\}$,$B=\left\{{\left.x\right|\frac{1}{4}≤{2^x}≤4}\right\}$,则A∩B=( )
| A. | {x|-1≤x≤2} | B. | {-1,0,1,2} | C. | {-2,-1,0,1,2} | D. | {0,1,2} |
1.(a+x)(1-x)4的展开式中x的奇数次幂项的系数之和为32,则a的值为( )
| A. | -3 | B. | 3 | C. | -5 | D. | 5 |
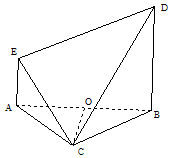 如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O为AB的中点.
如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O为AB的中点.