题目内容
8．设函数F（x）=$\frac{f（x）}{e^x}$是定义在R上的函数，其中f（x）的导函数为f'（x），满足f'（x）＜f（x）对于x∈R恒成立，则（ ）| A． | f（2）＞e2f（0），f（2 017＞e2017f（0） | B． | f（2）＞e2f（0），f（2 017）＜e2017f（0） | ||
| C． | f（2）＜e2f（0），f（2 017）＞e2017f（0） | D． | f（2）＜e2f（0），f（2 017）＜e2017f（0） |
分析 对f（x）求导，利用f'（x）＜f（x）得到单调性，利用单调性求2与0以及2017与0的函数值的大小．
解答 解：F'（x）=[$\frac{f（x）}{e^x}$]'=$\frac{f'（x）{e}^{x}-f（x）{e}^{x}}{（{e}^{x}）^{2}}=\frac{f'（x）-f（x）}{{e}^{x}}$，因为f'（x）＜f（x），
所以F'（x）＜0，所以F（x）为减函数，
因为2＞0，2017＞0，
所以F（2）＜F（0），F（2017）＜F（0），
即$\frac{f（2）}{{e}^{2}}＜\frac{f（0）}{{e}^{0}}$，所以f（2）＜e2f（0）；
$\frac{f（2017）}{{e}^{2017}}＜\frac{f（0）}{{e}^{0}}$，即f（2017）＜e2017f（0）；
故选D．
点评 本题考查了利用函数的单调性判断函数值的大小关系；关键是正确判断F（x）的单调性，并正确运用．
练习册系列答案
相关题目
18．已知函数$f（x）=\frac{{{e^x}+{e^{-x}}+sinx}}{{{e^x}+{e^{-x}}}}$，其导函数记为f'（x），则f（2017511）+f'（2017511）+f（-2017511）-f'（-2017511）=（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 2017511 |
19．在数列{an}中，a1=1，an=$\frac{n-1}{n}$an-1（n≥2），则通项公式an等于（ ）
| A． | $\frac{n-1}{n}$ | B． | $\frac{1}{n}$ | C． | $\frac{n}{n-1}$ | D． | $\frac{n+1}{n}$ |
16．已知集合A={x|x2-6x+5≤0}，B={x||2x-3|＜1}，则A∩B=（ ）
| A． | （1，2） | B． | [1，2） | C． | （2，5] | D． | [2，5] |
3．设集合A={-1，1，2，3}，集合B={-2，-1，0，1}则A∩B=（ ）
| A． | {-2，-1，1，2} | B． | {-1，1} | C． | {2} | D． | {1} |
13．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积为（ ）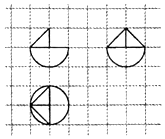
| A． | $\frac{2π+1}{3}$ | B． | $\frac{4π+1}{3}$ | C． | $\frac{2π+3}{3}$ | D． | $\frac{2π+2}{3}$ |
20．已知集合$A=\left\{{\left.{x∈Z}\right|\frac{4-x}{x+2}≥0}\right\}$，$B=\left\{{\left.x\right|\frac{1}{4}≤{2^x}≤4}\right\}$，则A∩B=（ ）
| A． | {x|-1≤x≤2} | B． | {-1，0，1，2} | C． | {-2，-1，0，1，2} | D． | {0，1，2} |
17．已知双曲线C1：$\frac{x^2}{4}-\frac{y^2}{3}=1$与双曲线C2：$\frac{x^2}{4}-\frac{y^2}{3}=-1$，给出下列说法，其中错误的是（ ）
| A． | 它们的焦距相等 | B． | 它们的焦点在同一个圆上 | ||
| C． | 它们的渐近线方程相同 | D． | 它们的离心率相等 |