题目内容
已知椭圆方程
+
=1（a＞b＞0），A（m，0）为椭圆外一定点，过A作直线l交椭圆于P、Q两点，且有|
|=λ|
|，Q关于x轴的对称点为B，x轴上一点C，当l变化时，证明：点C在BP上的充要条件是C的坐标为（
，0）．
| x2 |
| a2 |
| y2 |
| b2 |
| AP |
| AQ |
| a2 |
| m |
考点：椭圆的简单性质
专题：圆锥曲线中的最值与范围问题
分析：连接AB，由于B、Q关于x轴对称，可得|
|=|
|，
=
=λ，
=λ
，
=λ
．设P（x1，y1），Q（x2，y2），C（x0，0），则B（x2，-y2），利用向量相等及
+
=1，
+
=1，可得
=λ2-1，即可得出点C的坐标为（
，0）．
| AQ |
| AB |
|
| ||
|
|
|
| ||
|
|
| AP |
| AQ |
| PC |
| CB |
| ||
| a2 |
| ||
| b2 |
| ||
| a2 |
| ||
| b2 |
| (x1+λx2)(λx2-x1) |
| a2 |
| a2 |
| m |
解答：
证明：连接AB，
∵B、Q关于x轴对称，
∴|
|=|
|，
又
=
=λ，依题意
与
同向，
与
同向，
∴
=λ
，
=λ
．
设P（x1，y1），Q（x2，y2），C（x0，0），则B（x2，-y2），
可得y1=λy2，x1-m=λ（x2-m）①，
x0-x1=λ（x2-x0）②，
又
+
=1，
+
=1，
∴
=λ2-1③，
将①②代入③中得x0=
，
∴点C的坐标为（
，0），
由于上述解题过程可逆，∴C在BP上的充要条件是C的坐标为（
，0）．
∵B、Q关于x轴对称，
∴|
| AQ |
| AB |
又
|
| ||
|
|
|
| ||
|
|
| AP |
| AQ |
| PC |
| CB |
∴
| AP |
| AQ |
| PC |
| CB |
设P（x1，y1），Q（x2，y2），C（x0，0），则B（x2，-y2），
可得y1=λy2，x1-m=λ（x2-m）①，
x0-x1=λ（x2-x0）②，
又
| ||
| a2 |
| ||
| b2 |
| ||
| a2 |
| ||
| b2 |
∴
| (x1+λx2)(λx2-x1) |
| a2 |
将①②代入③中得x0=
| a2 |
| m |
∴点C的坐标为（
| a2 |
| m |
由于上述解题过程可逆，∴C在BP上的充要条件是C的坐标为（
| a2 |
| m |
点评：本题考查了椭圆的标准方程及其性质、向量运算、充要条件，考查了推理能力与计算能力，属于难题．
练习册系列答案
相关题目
在平行六面体ABCD-A1B1C1D1中，以顶点A为端点的三条棱长都是1，且夹角都是60°，则相对的面AD1与面BC1的距离为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
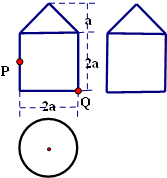一个几何体的三视图及部分度量值如图所示，其中，正视图与侧视图都是由一个正方形和一个等腰三角形组成，俯视图是一个圆．