题目内容
 如图,在△ABC中,BC=1,AB=2,∠ABC=60°,四边形ACDE为矩形,且平面ACDE⊥平面ABC,DC=1.
如图,在△ABC中,BC=1,AB=2,∠ABC=60°,四边形ACDE为矩形,且平面ACDE⊥平面ABC,DC=1.(Ⅰ)求证:BC⊥平面ACDE;
(Ⅱ)若点M为线段ED的中点,求平面MAB与平面BCD所成锐二面角的正切值.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由在△ABC中,BC=1,AB=2,∠ABC=60°,结合余弦定理和勾股定理,可得BC⊥AC,结合平面ACDE⊥平面ABC和面面垂直的性质定理可得:BC⊥平面ACDE;
(II)(综合几何法)延长CD、AM交于一点F,连FB,过C作CG⊥FB于点G,连AG.由于BC⊥AC,DC⊥AC,故AC⊥平面BCF,于是AC⊥FB,又CG⊥FB,故AG⊥FB,于是∠CGA为所求角,解三角形可得答案;
(向量法)如图平面直角坐标系,设平面MAB与平面BCD所成锐二面角为θ,分别求出两个平面的法向量,代入向量夹角公式,可得答案.
(II)(综合几何法)延长CD、AM交于一点F,连FB,过C作CG⊥FB于点G,连AG.由于BC⊥AC,DC⊥AC,故AC⊥平面BCF,于是AC⊥FB,又CG⊥FB,故AG⊥FB,于是∠CGA为所求角,解三角形可得答案;
(向量法)如图平面直角坐标系,设平面MAB与平面BCD所成锐二面角为θ,分别求出两个平面的法向量,代入向量夹角公式,可得答案.
解答:
证明:(I)由BC=1,AB=2,∠ABC=60°,
由余弦定理可得:AC2=AB2+BC2-2AB•BC•cos∠ABC=4+1-2=3=AB2-BC2,
∴BC⊥AC,
又平面ACDE⊥平面ABC,平面ACDE∩平面ABC=AC,BC?平面ABC,
∴BC⊥平面ACDE;
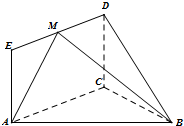
解:(II)(综合几何法)延长CD、AM交于一点F,连FB,过C作CG⊥FB于点G,连AG.
由于BC⊥AC,DC⊥AC,故AC⊥平面BCF,
于是AC⊥FB,又CG⊥FB,故AG⊥FB,于是∠CGA为所求角,
由M是AF的中点,于是CF=2,故CG=
=
,
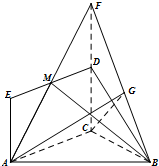
于是在△ACG中,tan∠CGA=
=
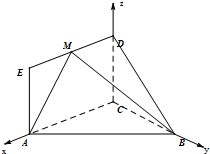
(向量法)如图建立平面直角坐标系,设所求角为θ,
则C(0,0,0),M(
,0,1),A(
,0,0),B(0,1,0),
=(-
,1,0),
=(-
,0,1),
设平面AMB的法向量
=(x1,y1,z1),于是
•
=0,
•
=0,
即-
x1+y1=0,-
x1+z1=0,令x1=1,则y1=
,z1=
,于是
=(1,
,
).
易得平面DCB的法向量
=(1,0,0),
于是cosθ=
=
,于是tanθ═
由余弦定理可得:AC2=AB2+BC2-2AB•BC•cos∠ABC=4+1-2=3=AB2-BC2,
∴BC⊥AC,
又平面ACDE⊥平面ABC,平面ACDE∩平面ABC=AC,BC?平面ABC,
∴BC⊥平面ACDE;

解:(II)(综合几何法)延长CD、AM交于一点F,连FB,过C作CG⊥FB于点G,连AG.
由于BC⊥AC,DC⊥AC,故AC⊥平面BCF,
于是AC⊥FB,又CG⊥FB,故AG⊥FB,于是∠CGA为所求角,
由M是AF的中点,于是CF=2,故CG=
| BC•CF |
| BF |
| 2 | ||
|

于是在△ACG中,tan∠CGA=
| AC |
| CG |
| ||
| 2 |
(向量法)如图建立平面直角坐标系,设所求角为θ,
则C(0,0,0),M(
| ||
| 2 |
| 3 |
| AB |
| 3 |
| AM |
| ||
| 2 |

设平面AMB的法向量
| n1 |
| n1 |
| AB |
| n1 |
| AM |
即-
| 3 |
| ||
| 2 |
| 3 |
| ||
| 2 |
| n1 |
| 3 |
| ||
| 2 |
易得平面DCB的法向量
| n2 |
于是cosθ=
| ||||
|
|
| 2 | ||
|
| ||
| 2 |
点评:本题考查的知识点是直线与平面垂直的判断,面面垂直的性质,二面的平面角及求法,是空间线面关系和线面夹角的综合应用,难度中档.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
某市进行一次高三教学质量抽样检测,考试后统计的所有考生的数学成绩服从正态分布.已知数学成绩平均分为90分,60分以下的人数占10%,则数学成绩在90分至120分之间的考生人数所占百分比约为( )
| A、10% | B、20% |
| C、30% | D、40% |
若(1-2x)2012=a0+a1x+a2x2+…+a2012x2012,则(a0+a1)+(a1+a2)+(a2+a3)+…+(a2011+a2012)=( )
| A、1 |
| B、22012 |
| C、1-22012 |
| D、2-22012 |