题目内容
12.已知x,y满足约束条件$\left\{\begin{array}{l}{x-2≥0}\\{x+y≤6}\\{2x-y≤6}\end{array}\right.$则目标函数z=$\frac{2y}{x+2}$的最大值为2.分析 画出约束条件的可行域,化简目标函数,利用目标函数的几何意义转化求解即可.
解答 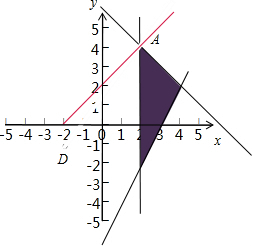 解:x,y满足约束条件$\left\{\begin{array}{l}{x-2≥0}\\{x+y≤6}\\{2x-y≤6}\end{array}\right.$,表示的可行域如图:
解:x,y满足约束条件$\left\{\begin{array}{l}{x-2≥0}\\{x+y≤6}\\{2x-y≤6}\end{array}\right.$,表示的可行域如图:
目标函数z=$\frac{2y}{x+2}$,目标函数的几何意义是可行域的点与(-2,0)斜率的2倍,
由题意可知:DA的斜率最大.
由$\left\{\begin{array}{l}{x=2}\\{x+y=6}\end{array}\right.$,可得A(2,4),
则目标函数的最大值为:$z=\frac{2×4}{2+2}$=2.
故答案为:2.
点评 本题考查线性规划的简单应用,考查数形结合以及转化思想的应用,考查计算能力.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
3.已知定义在R上的函数y=f(x)满足:①对于任意的x∈R,都有f(x+2)=f(x-2);②函数y=f(x+2)是偶函数;③当x∈(0,2]时,f(x)=ex-$\frac{1}{x}$,a=f(-5),b=f($\frac{19}{2}$).c=f($\frac{41}{4}$),则a,b,c的大小关系是( )
| A. | a<b<c | B. | c<a<b | C. | c<a<b | D. | b<a<c |
20.若函数$f(x)=a({x-2}){e^x}+lnx+\frac{1}{x}$在(0,2)上存在两个极值点,则a的取值范围是( )
| A. | (-∞,-$\frac{1}{4{e}^{2}}$) | B. | (-∞,-$\frac{1}{e}$) | ||
| C. | (-∞,-$\frac{1}{e}$)∪(-$\frac{1}{e}$,-$\frac{1}{4{e}^{2}}$) | D. | (-e,-$\frac{1}{4{e}^{2}}$)∪(1,+∞) |
7.设命题p:?x∈R,ex≥x+1,则¬p为( )
| A. | ?x∈R,ex<x+1 | B. | ?x0∈R,ex0<x0+1 | C. | ?x0∈R,ex0≤x0+1 | D. | ?x∈R,ex0≥x0+1 |