题目内容
2.已知函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{2}(1-x)|,x<1}\\{-{x}^{2}+4x-2,x≥1}\end{array}\right.$则方程f(x+$\frac{1}{x}$-2)=1的实根个数为( )| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
分析 令g(x)=x+$\frac{1}{x}$-2,则g(x)=1或3或-1或$\frac{1}{2}$,再根据g(x)的图象判断各个方程的根的个数即可.
解答 解:令f(x)=1得x=3或x=1或x=$\frac{1}{2}$或x=-1,
∵f(x+$\frac{1}{x}$-2)=1,
∴x+$\frac{1}{x}$-2=3或x+$\frac{1}{x}$-2=1或x+$\frac{1}{x}$-2=$\frac{1}{2}$或x+$\frac{1}{x}$-2=-1.
令g(x)=x+$\frac{1}{x}$-2,则当x>0时,g(x)≥2-2=0,
当x<0时,g(x)≤-2-2=-4,
作出g(x)的函数图象如图所示: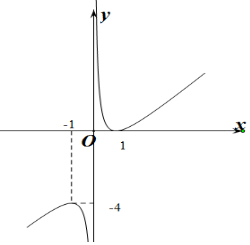
∴方程x+$\frac{1}{x}$-2=3,x+$\frac{1}{x}$-2=1,x+$\frac{1}{x}$-2=$\frac{1}{2}$均有两解,
方程x+$\frac{1}{x}$-2=-1无解.
∴方程f(x+$\frac{1}{x}$-2)=1有6解.
故选C.
点评 本题考查了方程根与函数图象的关系,属于中档题.

练习册系列答案
相关题目
13.“=”在基本算法语句中叫( )
| A. | 赋值号 | B. | 等号 | C. | 输入语句 | D. | 输出语句 |
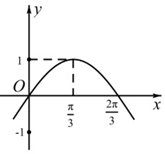 已知函数f(x)=Asin(ωx+$\frac{π}{6}$)-1(A>0,ω>0)的部分图象如图,则对于区间[0,π]内的任意实数x1,x2,f(x1)-f(x2)的最大值为( )
已知函数f(x)=Asin(ωx+$\frac{π}{6}$)-1(A>0,ω>0)的部分图象如图,则对于区间[0,π]内的任意实数x1,x2,f(x1)-f(x2)的最大值为( )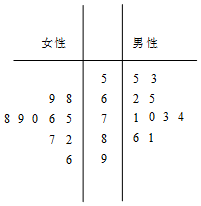 某城市为了满足市民出行的需要和节能环保的要求,在公共场所提供单车共享服务,某部门为了对该城市共享单车进行监管,随机选取了20位市民对共享单车的情况进行问卷调查,并根据其满意度评分值(满分100分)制作的茎叶图如图所示:
某城市为了满足市民出行的需要和节能环保的要求,在公共场所提供单车共享服务,某部门为了对该城市共享单车进行监管,随机选取了20位市民对共享单车的情况进行问卷调查,并根据其满意度评分值(满分100分)制作的茎叶图如图所示: