题目内容

11．设集合S={x|x＜-5或x＞5}，T={x|-7＜x＜3}，则S∩T=（　　）
A．{x|-7＜x＜-5}B．{x|3＜x＜5}C．{x|-5＜x＜3}D．{{x|-7＜x＜5}

分析 利用交集定义和不等式性质求解．

解答 解：∵集合S={x|x＜-5或x＞5}，T={x|-7＜x＜3}，
∴S∩T={x|-7＜x＜-5}．
故选：A．

点评 本题考查交集的求法，解题时要认真审题，是基础题．

练习册系列答案
相关题目
1．计算：log29•log38=（　　）
A．6B．8C．10D．1
2．给出下列六个命题：
①两个向量相等，则它们的起点相同，终点相同；
②若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|，则$\overrightarrow{a}$=$\overrightarrow{b}$；
③若$\overrightarrow{AB}$=$\overrightarrow{DC}$，则A，B，C，D四点构成平行四边形；
④在平行四边形ABCD中，一定有$\overrightarrow{AB}$=$\overrightarrow{DC}$；
⑤若$\overrightarrow{m}$=$\overrightarrow{n}$，$\overrightarrow{n}$=$\overrightarrow{p}$，则$\overrightarrow{m}$=$\overrightarrow{p}$；
⑥若向$\overrightarrow{a}$∥$\overrightarrow{b}$，$\overrightarrow{b}$∥$\overrightarrow{c}$，则$\overrightarrow{a}$∥$\overrightarrow{c}$．
其中错误的命题有①②③⑥．（填序号）
19．下列说法中错误的是（　　）
A．垂直于同一条直线的两条直线相互垂直
B．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行
C．若一个平面经过另一个平面的垂线，那么这两个平面相互垂直
D．若一个平面内的两条相交直线与另一个平面内的相交直线分别平行，那么这两个平面相互平行
6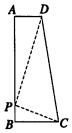．如图所示，在直角梯形ABCD中，AB=7，AD=2，BC=3．如果AB边上的点P使得以P，A，D为顶点的三角形和以P，B，C为顶点的三角形相似，那么这样的点P有（　　）
A．1个B．2个C．3个D．2个
16．若“$?x∈[{0，\frac{π}{3}}]，m≥2tanx$”是真命题，则实数m的最小值为2$\sqrt{3}$．
3．若不等式（a2-3a-4）x2-（a-4）x-1＜0的解集为R，则实数a的取值范围为（　　）
A．（0，4）B．（0，4]C．[0，4）D．[0，4]
11．椭圆的对称中心在坐标原点，一个顶点为A（0，2），右焦点F与点$B（\sqrt{2}，\sqrt{2}）$的距离为2，
（1）求椭圆的方程；
（2）斜率k≠0的直线l：y=kx-2与椭圆相交于不同的两点M，N满足|AM|=|AN|，求直线l的方程．
12．△ABC中，角A，B，C的对边分别为a，b，c，已知$b=\frac{1}{2}$，$bsinA=asin\frac{B}{2}$，则S△ABC的最大值为（　　）
A．$\frac{{\sqrt{3}}}{8}$B．$\frac{{\sqrt{3}}}{16}$C．$\frac{{\sqrt{3}}}{24}$D．$\frac{{\sqrt{3}}}{48}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网