题目内容
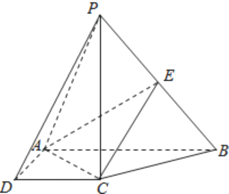
【题目】如图，在四棱锥P－ABCD中，四边形ABCD是矩形，侧面PAD⊥底面ABCD，若点E，F分别是PC，BD的中点。
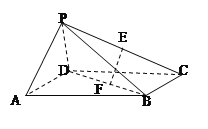
（1）求证：EF∥平面PAD；
（2）求证：平面PAD⊥平面PCD
【答案】（1）详见解析，（2）详见解析.
【解析】试题分析：（1）本题考察的是直线和平面平行的证明，一般采用线线平行或者面面平行的方法来证明．本题中利用三角形中位线的性质，可得线线平行，证明
为平行四边形，可得
∥
，从而得到线面平行．
（2）本题证明的是面面垂直，需要先证明线面垂直，再通过面面垂直判断定理，即可得到面面垂直．
试题解析：（1）设
中点为
，
中点为
，连结
，
为中点，
为
中点，
，
同理
，
为矩形，
，，为平行四边形，
∥，
又
∥面
（用
证明当然可以）
（2）面⊥面，面
面＝，又为矩形，
，⊥面，
又
面
，面⊥面．
练习册系列答案
相关题目
