题目内容
【题目】已知二次函数![]() 的对称轴为
的对称轴为![]() ,
,![]() .
.
(1)求函数![]() 的最小值及取得最小值时
的最小值及取得最小值时![]() 的值;
的值;
(2)试确定![]() 的取值范围,使
的取值范围,使![]() 至少有一个实根;
至少有一个实根;
(3)若![]() ,存在实数
,存在实数![]() ,对任意
,对任意![]() ,使
,使![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,此时
,此时![]() ;(2)
;(2)![]() 的取值范围为
的取值范围为![]() ;(3)实数
;(3)实数![]() 的取值范围为
的取值范围为![]() .
.
【解析】
试题分析:(1)利用基本不等式易得![]() ,此时
,此时![]() .(2)
.(2)![]() 至少有一个实根,即
至少有一个实根,即![]() 与
与![]() 的图象在
的图象在![]() 上至少有一个交点,由题意,可得
上至少有一个交点,由题意,可得![]() ,
,![]() ,则需
,则需![]() 即可;(3)由题意,可得
即可;(3)由题意,可得![]() ,则
,则![]() ,
,
由已知存在实数![]() ,对任意
,对任意![]() ,使
,使![]() 恒成立.即
恒成立.即![]() .令
.令![]() ∴
∴![]() ,转化为存在
,转化为存在![]() ,使
,使![]() 成立.令
成立.令![]() ,
,![]() 的对称轴为
的对称轴为![]() ,分类讨论,即可得到实数
,分类讨论,即可得到实数![]() 的取值范围
的取值范围
试题解析:(1)∵![]() ,∴
,∴![]() ,
,
∴![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时“=”成立,即
时“=”成立,即![]() ,此时
,此时![]() .
.
(2)![]() 的对称轴为
的对称轴为![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
![]() 至少有一个实根,∴
至少有一个实根,∴![]() 至少有一个实根,
至少有一个实根,
即![]() 与
与![]() 的图象在
的图象在![]() 上至少有一个交点,
上至少有一个交点,
![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() 的取值范围为
的取值范围为![]() .
.
(3)![]() ,∴
,∴![]() ,
,
由已知存在实数![]() ,对任意
,对任意![]() ,使
,使![]() 恒成立.
恒成立.
∴![]() .
.
令![]() ,∴
,∴![]() ,即
,即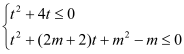 ,
,
转化为存在![]() ,使
,使![]() 成立.
成立.
令![]() ,∴
,∴![]() 的对称轴为
的对称轴为![]() ,
,
∵![]() ,∴
,∴![]() .
.
①当![]() ,即
,即![]() 时,
时,
![]() ,
,
∴![]() ,∴
,∴![]() .
.
②当![]() ,即
,即![]() 时,
时,
![]() ,
,
∴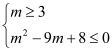 ,∴
,∴![]() ,∴
,∴![]() .
.
综上,实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目