题目内容
已知集合M={-1，0，1}，N={x|0≤log2x≤1，x∈Z}，则M∩N=（ ）
| A、{0，1} | B、{-1，0} |
| C、{0} | D、{1} |
考点：交集及其运算
专题：集合
分析：利用交集的性质和对数函数的性质求解．
解答：
解：∵集合M={-1，0，1}，N={x|0≤log2x≤1，x∈Z}={1，2}，
∴M∩N={1}．
故选：D．
∴M∩N={1}．
故选：D．
点评：本题考查交集的求法，是基础题，解题时要注意对数函数的性质的合理运用．
练习册系列答案
相关题目
已知两个向量
=（t，
），
=（x+1，
），其中t，u都是正实数，且
=2
，则
的取值范围是（ ）
| a |
| x |
| b |
| u |
| 2 |
| a |
| b |
| t |
| u |
| A、[1，6] |
| B、[-6，1] |
| C、[4，+∞） |
| D、（-∞，1] |
函数y=lg（x-5）的定义域为M，函数y=lg（x-5）+lg（12-x）的定义域为N，则（ ）
| A、M∪N=R | B、M=N |
| C、M?N | D、M⊆N |
命题“?x∈（0，+∞），x+
≥4”的否定为（ ）
| 4 |
| x |
A、?x∈（0，+∞），x+
| ||
B、?x∈（0，+∞），x+
| ||
C、?x∈（0，+∞），x+
| ||
D、?x∈（0，+∞），x+
|
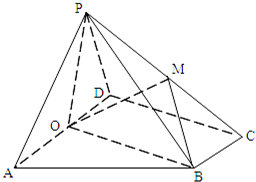如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，O为AD中点，M是棱PC上的点，AD=2BC．
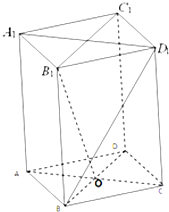如图，四棱柱中A1B1C1D1-ABCD，底面ABCD为边长为2的菱形，侧棱长为3，且∠B1BA=∠B1BC=∠ABC=60°．