题目内容
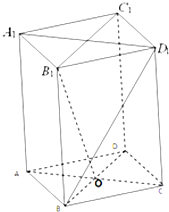如图，四棱柱中A1B1C1D1-ABCD，底面ABCD为边长为2的菱形，侧棱长为3，且∠B1BA=∠B1BC=∠ABC=60°．（1）求证：AC⊥平面B1BDD1
（2）求BC1与平面ABCD所成角的正弦值．
考点：直线与平面所成的角,直线与平面垂直的判定
专题：空间位置关系与距离,空间角
分析：法一：
（Ⅰ）由菱形性质得AC⊥BD，由向量性质得AC⊥B1B，由此能证明AC⊥平面B1BDD1．
（Ⅱ）以O为原点，以DB为x轴、AC为y轴、OB1为z轴，建立空间直角坐标系，利用向量法能求出BC1与平面ABCD所成角的正弦值．
法二：
（Ⅰ）证明：∵四边形ABCD为边长为菱形，∴AC⊥BD．
又∵AB=BC，∠B1BA=∠B1BC，B1B=B1B，
∴△ABB1≌△CBB1，B1A=B1C．
而菱形ABCD对角线交点O为AC的中点，∴B1O⊥AC
∴AC⊥平面B1BDD1（4分）
（Ⅱ）设菱形A1B1C1D1对角线的交点为O1，连接O1O，则∠O1OD为平面A1ACC1与平面ABCD所成二面角的平面角，由此能求出BC1与平面ABCD所成角的正弦值．
（Ⅰ）由菱形性质得AC⊥BD，由向量性质得AC⊥B1B，由此能证明AC⊥平面B1BDD1．
（Ⅱ）以O为原点，以DB为x轴、AC为y轴、OB1为z轴，建立空间直角坐标系，利用向量法能求出BC1与平面ABCD所成角的正弦值．
法二：
（Ⅰ）证明：∵四边形ABCD为边长为菱形，∴AC⊥BD．
又∵AB=BC，∠B1BA=∠B1BC，B1B=B1B，
∴△ABB1≌△CBB1，B1A=B1C．
而菱形ABCD对角线交点O为AC的中点，∴B1O⊥AC
∴AC⊥平面B1BDD1（4分）
（Ⅱ）设菱形A1B1C1D1对角线的交点为O1，连接O1O，则∠O1OD为平面A1ACC1与平面ABCD所成二面角的平面角，由此能求出BC1与平面ABCD所成角的正弦值．
解答：
解法一：
（Ⅰ）证明：∵四边形ABCD为边长为菱形，∴AC⊥BD
又∵
•
=（
+
）•
=
•
+
•
，
而
•
=-
•
=-|
|•|
|cos60°=-3，
•
=
•
=|
|•|
|cos60°=3，
∴
•
=0，即AC⊥B1B，
又BD∩B1B=B，∴AC⊥平面B1BDD1．（4分）
（Ⅱ）解：∵∠ABC=60°，AB=BC=2，∴BO=
，
在△ABB1中，B1A2=AB2+B1B2-2AB×B1Bcos60°=7，
在直角△B1OA中，B1O2=B1A2-OA2=6，B1O=
，
∴B1O2+BO2=9=B1B2，
∴∠B1OB=90°，B1O⊥BO．（10分）
∴以O为原点，以DB为x轴、AC为y轴、OB1为z轴，
建立空间直角坐标系，A（0，-1，0），D1（-2
，0，
），
∵BC1∥AD1，∴BC1与平面ABCD所成角等于AD1与平面ABCD所成角，设这个为角θ，
而
=（-2
，1，
），平面ABCD的法向量
=（0，0，1）
∴cos＜
，
＞=
=
=
，＜
，
＞＜
．
∴θ=
-＜
，
＞，
BC1与平面ABCD所成角的正弦值sinθ=cos＜
，
＞=
．（12分）
解法二：
（Ⅰ）证明：∵四边形ABCD为边长为菱形，∴AC⊥BD．
又∵AB=BC，∠B1BA=∠B1BC，B1B=B1B，
∴△ABB1≌△CBB1，B1A=B1C．
而菱形ABCD对角线交点O为AC的中点，∴B1O⊥AC
∴AC⊥平面B1BDD1（4分）
（Ⅱ）解：设菱形A1B1C1D1对角线的交点为O1，
连接O1O，则O1O∥B1B，∠O1OD=∠B1BD
由知AC⊥平面B1BDD1，∴AC⊥O1O，又BD⊥AC
∴∠O1OD为平面A1ACC1与平面ABCD所成二面角的平面角，（6分）
∵∠ABC=60°，AB=BC=2，∴BO=
，
在△ABB1中，B1A2=AB2+B1B2-2AB×B1Bcos60°=7
在直角△B1OA中，B1O2=B1A2-OA2=6，B1O=
，
∴B1O2+BO2=9=B1B2，∴∠B1OB=90°，B1O⊥BO
∴B1O⊥平面ABCD，∴平面B1AC⊥平面ABCD
连接BC1交B1C于E，E就为BC1的中点．
在△B1OC中，作EF⊥OC，垂足为F，连接BF，则EF∥B1O，EF⊥平面ABCD，
∠EBF就为BC1与平面ABCD所成角，（10分）
∴EF⊥BF，EF=
B1O=
，而BF2=OF2+OB2=
，BE2=EF2+BF2=
，BE=
，
∴BC1与平面ABCD所成角的正弦值sin∠EBF=
=
．（12分）
（Ⅰ）证明：∵四边形ABCD为边长为菱形，∴AC⊥BD
又∵
| AC |
| B1B |
| AB |
| AD |
| B1B |
| AB |
| B1B |
| AD |
| B1B |
而
| AB |
| B1B |
| BA |
| B1B |
| BA |
| B1B |
| AD |
| B1B |
| BC |
| B1B |
| BC |
| B1B |
∴
| AC |
| B1B |
又BD∩B1B=B，∴AC⊥平面B1BDD1．（4分）
（Ⅱ）解：∵∠ABC=60°，AB=BC=2，∴BO=
| 3 |
在△ABB1中，B1A2=AB2+B1B2-2AB×B1Bcos60°=7，
在直角△B1OA中，B1O2=B1A2-OA2=6，B1O=
| 6 |
∴B1O2+BO2=9=B1B2，
∴∠B1OB=90°，B1O⊥BO．（10分）
∴以O为原点，以DB为x轴、AC为y轴、OB1为z轴，
建立空间直角坐标系，A（0，-1，0），D1（-2
| 3 |
| 6 |
∵BC1∥AD1，∴BC1与平面ABCD所成角等于AD1与平面ABCD所成角，设这个为角θ，
而
| AD1 |
| 3 |
| 6 |
| n |
∴cos＜
| n |
| AD1 |
| ||||
|
|
| ||
|
| ||
| 19 |
| n |
| AD1 |
| π |
| 2 |
∴θ=
| π |
| 2 |
| n |
| AD1 |
BC1与平面ABCD所成角的正弦值sinθ=cos＜
| n |
| AD1 |
| ||
| 19 |
解法二：
（Ⅰ）证明：∵四边形ABCD为边长为菱形，∴AC⊥BD．
又∵AB=BC，∠B1BA=∠B1BC，B1B=B1B，
∴△ABB1≌△CBB1，B1A=B1C．
而菱形ABCD对角线交点O为AC的中点，∴B1O⊥AC
∴AC⊥平面B1BDD1（4分）
（Ⅱ）解：设菱形A1B1C1D1对角线的交点为O1，
连接O1O，则O1O∥B1B，∠O1OD=∠B1BD
由知AC⊥平面B1BDD1，∴AC⊥O1O，又BD⊥AC
∴∠O1OD为平面A1ACC1与平面ABCD所成二面角的平面角，（6分）
∵∠ABC=60°，AB=BC=2，∴BO=
| 3 |
在△ABB1中，B1A2=AB2+B1B2-2AB×B1Bcos60°=7
在直角△B1OA中，B1O2=B1A2-OA2=6，B1O=
| 6 |
∴B1O2+BO2=9=B1B2，∴∠B1OB=90°，B1O⊥BO
∴B1O⊥平面ABCD，∴平面B1AC⊥平面ABCD
连接BC1交B1C于E，E就为BC1的中点．
在△B1OC中，作EF⊥OC，垂足为F，连接BF，则EF∥B1O，EF⊥平面ABCD，
∠EBF就为BC1与平面ABCD所成角，（10分）
∴EF⊥BF，EF=
| 1 |
| 2 |
| ||
| 2 |
| 13 |
| 4 |
| 19 |
| 4 |
| ||
| 2 |
∴BC1与平面ABCD所成角的正弦值sin∠EBF=
| ||||
|
| ||
| 19 |
点评：本题考查直线与平面垂直的证明，考查直线与平面所成角的正弦值的求法，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
学业测评一课一测系列答案
相关题目
已知x∈R，则“x2-3x≤0”是“（x-1）（x-2）≤0成立”的（ ）
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知集合M={-1，0，1}，N={x|0≤log2x≤1，x∈Z}，则M∩N=（ ）
| A、{0，1} | B、{-1，0} |
| C、{0} | D、{1} |
已知向量
=（1，1，0），
=（-1，0，2），且k
+
与
互相垂直，则k的值是（ ）
| a |
| b |
| a |
| b |
| b |
| A、-5 | ||
B、
| ||
C、
| ||
| D、5 |
如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD的边BC垂直于圆O所在的平面．