题目内容
9.数轴上有四个间隔为1的点依次记为A、B、C、D,在线段AD上随机取一点E,则E点到B、C两点的距离之和小于2的概率为$\frac{2}{3}$.分析 求出满足条件的E点所在的位置,从而求出E点到B、C两点的距离之和小于2的概率即可.
解答 解:设AB的中点是M,CD的中点是N,
则E在MN上时满足条件,
故E点到B、C两点的距离之和小于2的概率p=$\frac{2}{3}$,
故答案为:$\frac{2}{3}$.
点评 本题考查了几何概型问题,考查线段的比值,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.函数f(x)是定义在R上的奇函数,且f(x-1)为偶函数,当x∈[0,1]时,$f(x)={x^{\frac{1}{2}}}$,若函数g(x)=f(x)-x-b恰有一个零点,则实数b的取值集合是( )
| A. | $(2k-\frac{1}{4},2k+\frac{1}{4}),k∈Z$ | B. | $(2k+\frac{1}{2},2k+\frac{5}{2}),k∈Z$ | ||
| C. | $(4k-\frac{1}{4},4k+\frac{1}{4}),k∈Z$ | D. | $(4k+\frac{1}{4},4k+\frac{15}{4}),k∈Z$ |
1.已知{an}是等比数列,且 ${a_5}=\frac{1}{2},4{a_3}+{a_7}=2$,则a9=( )
| A. | 2 | B. | ±2 | C. | 8 | D. | $\frac{1}{8}$ |
18.已知F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,过F作倾斜角为60°的直线l,直线l与双曲线交于A,与y轴交于点B,且$\overrightarrow{FA}$=$\frac{1}{2}$$\overrightarrow{FB}$,则该双曲线的离心率等于( )
| A. | $\sqrt{3}$+1 | B. | $\frac{\sqrt{3}+1}{2}$ | C. | $\frac{\sqrt{3}}{2}$+1 | D. | $\frac{\sqrt{3}-1}{4}$ |
19.已知命题p:?x∈R,x2-x+1≤0,则( )
| A. | ¬p:?x0∈R,x02-x0+1≤0 | B. | ¬p:?x∈R,x2-x+1≥0 | ||
| C. | ¬p:?x∈R,x2-x+1>0 | D. | ¬p:?0x∈R,x02-x0+1>0 |
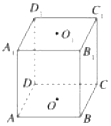 如图所示,在正方体ABCD-A1B1C1D1中,O1、O为上、下底面的中心,在直线D1D、A1D、A1D1、C1D1、O1D与平面AB1C平行的直线有2条.
如图所示,在正方体ABCD-A1B1C1D1中,O1、O为上、下底面的中心,在直线D1D、A1D、A1D1、C1D1、O1D与平面AB1C平行的直线有2条.