��Ŀ����
8����֪Բ����x���ϵ�ԲC��ֱ��l��4x+3y-6=0���ڵ�M��$\frac{3}{5}$��$\frac{6}{5}$����1����ֱ��12x-5y-1=0��ԲC�صõ��ҳ�
��2����֪N��2��1��������ԭ�㣬��б��Ϊ������ֱ��L��ԲC����P��x1��y1����Q��x2��y2������
��i����֤��$\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}$Ϊ��ֵ
��ii����|PN|2+|QN|2=24����ֱ��L�ķ��̣�
���� ��1�������Բ�ķ��̣�����ֱ��12x-5y-1=0��ԲC�صõ��ҳ�
��2����i����ֱ��l�ķ���Ϊy=kx��k��0������Բ�ķ����������ɵã�1+k2��x2+2x-3=0������Τ�ﶨ������֤����
��ii����|PN|2+|QN|2=24������Τ�ﶨ�������ֱ�ߵ�б�ʣ�������ֱ��L�ķ��̣�
��� �⣺��1�������⣬C��a��0����z\��kCM=$\frac{\frac{6}{5}}{\frac{3}{5}-a}$��
��$\frac{\frac{6}{5}}{\frac{3}{5}-a}$•��-$\frac{4}{3}$��=-1����a=-1��
��C��-1��0����|CM|=2����r=2��
��ԲC�ı�����Ϊ��x+1��2+y2=4��
Բ�ĵ�ֱ��12x-5y-1=0�ľ���Ϊ1���������ҳ�Ϊ2$\sqrt{4-1}$=2$\sqrt{3}$��
��2����ֱ��l�ķ���Ϊy=kx��k��0������Բ�ķ����������ɵã�1+k2��x2+2x-3=0��
��x1+x2=-$\frac{2}{1+{k}^{2}}$��x1x2=-$\frac{3}{1+{k}^{2}}$��
��i��$\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{2}{3}$Ϊ��ֵ��
��ii��|PN|2+|QN|2=$��{x}_{1}-2��^{2}+��{y}_{1}-1��^{2}$+$��{x}_{2}-2��^{2}+��{y}_{2}-1��^{2}$
=$��1+{k}^{2}����{x}_{1}+{x}_{2}��^{2}-2��1+{k}^{2}��{x}_{1}{x}_{2}$-��4+2k����x1+x2��+10=$\frac{12+4k}{1+{k}^{2}}$+16=24��
��k=1��-$\frac{1}{2}$��
������k=1�������⣬
��ֱ��L�ķ���Ϊy=x��
���� ���⿼��Բ�ķ��̣�����ֱ����Բ��λ�ù�ϵ������Τ�ﶨ�������ã�����ѧ�������������������������е��⣮

 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�| A�� | ���ƽ�����ƽ�� �ã�ƽ��¡�ƽ�� �ã����ɦ�=l����ôl�ͦ� | |
| B�� | ���ƽ�����ƽ�� �£���ôƽ�����һ������ֱ��ƽ����ƽ��� | |
| C�� | ���ƽ�������ֱ��ƽ��£���ôƽ�����һ��������ֱ�ߴ�ֱ��ƽ��� | |
| D�� | ���ƽ�����ƽ�� �£�����������һ�������ߵĴ��ߣ���ô�˴��߱ش�ֱ�ڦ� |
| A�� | ��1��+�ޣ� | B�� | ��-�ޣ�-1�� | C�� | ��-1��1�� | D�� | ��-�ޣ�1���ȣ�1��+�ޣ� |
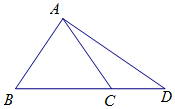 ��֪��ABC�ǵȱ������Σ�D��BC���ӳ����ϣ���CD=2��${S_{��ABD}}=6\sqrt{3}$��
��֪��ABC�ǵȱ������Σ�D��BC���ӳ����ϣ���CD=2��${S_{��ABD}}=6\sqrt{3}$��