题目内容
7.由约束条件$\left\{\begin{array}{l}x,y≥0\\ y≤-3x+3\\ y≤kx+1\end{array}\right.$,确定的可行域D能被半径为$\frac{{\sqrt{2}}}{2}$的圆面完全覆盖,则实数k的取值范围是$(-∞,\frac{1}{3}]$.分析 先画出由约束条件确定的可行域D,由可行域能被圆覆盖得到可行域是封闭的,判断出直线y=kx+1斜率小于等于$\frac{1}{3}$即可得出k的范围.
解答 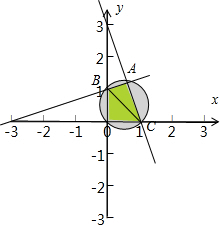 解:∵可行域能被圆覆盖,
解:∵可行域能被圆覆盖,
∴可行域是封闭的,
作出约束条件$\left\{\begin{array}{l}x,y≥0\\ y≤-3x+3\\ y≤kx+1\end{array}\right.$的可行域:
可得B(0,1),C(1,0),|BC|=$\sqrt{2}$,
结合图,要使可行域能被$\frac{\sqrt{2}}{2}$为半径的圆覆盖,
只需直线y=kx+1与直线y=-3x+3的交点坐标在圆的内部,
两条直线垂直时,交点恰好在圆上,此时k=$\frac{1}{3}$,
则实数k的取值范围是:$(-∞,\frac{1}{3}]$.
故答案为:$(-∞,\frac{1}{3}]$.
点评 本题考查画不等式组表示的平面区域、考查将图形的大小关系转化为不等式.

练习册系列答案
相关题目
18.用反证法证明命题:“三角形的内角中至少有一个不大于60°”的过程归纳为以下三个步骤:①因为A+B+C>60°+60°+60°=180°,这与三角形内角和为180°相矛盾;②所以一个三角形的内角中至少有一个不大于60°;③假设三角形的三个内角A、B、C都大于60°,正确顺序的序号为( )
| A. | ③①② | B. | ②③① | C. | ①③② | D. | ①②③ |
2.下面程序框图输出的结果是( )


| A. | 3 | B. | 12 | C. | 60 | D. | 360 |
12.执行如图所示的程序框图,则输出的结果为( )


| A. | 12 | B. | 11 | C. | 10 | D. | 9 |
 一个四面体的三视图如图所示,则该四面体的表面积是2$+\sqrt{3}$.
一个四面体的三视图如图所示,则该四面体的表面积是2$+\sqrt{3}$.