题目内容
15.已知$α,β∈({0,\frac{π}{2}})$,且$α+β≠\frac{π}{2},sinβ=sinαcos({α+β})$.(1)用tanα表示tanβ;
(2)求tanβ的最大值.
分析 (1)把已知等式的左边中的角β变为α+β-α,利用两角和与差的正弦函数公式化简,移项整理后,在等式左右两边同时除以cos(α+β)cosα,利用同角三角函数间的基本关系弦化切后,利用两角和的正切函数公式即可得解.
(2)由(1)及基本不等式即可计算得解.
解答 解:(1)∵α,β∈(0,$\frac{π}{2}$),
∴sinβ=sin(α+β-α)=cos(α+β)sinα,
即sin(α+β)cosα-cos(α+β)sinα=cos(α+β)sinα,
移项得:sin(α+β)cosα=2cos(α+β)sinα,
两边同时除以cos(α+β)cosα,得:tan(α+β)=2tanα,
∴$\frac{tanα+tanβ}{1-tanαtanβ}$=2tanα,可得:tanβ=$\frac{tanα}{1+2ta{n}^{2}α}$.
(2)∵$α,β∈({0,\frac{π}{2}})$,
∴由(1)可得tanβ=$\frac{tanα}{1+2ta{n}^{2}α}$=$\frac{1}{\frac{1}{tanα}+2tanα}$≤$\frac{\sqrt{2}}{4}$.
即tanβ的最大值为$\frac{\sqrt{2}}{4}$.
点评 此题考查了三角函数恒等变换的应用以及基本不等式的综合应用,熟练掌握公式及基本关系,灵活变换角度是解本题的关键,属于中档题.

练习册系列答案
相关题目
5.设p:实数x、y满足(x-1)2+(y-1)2≤1,q:实数x、y满足$\left\{\begin{array}{l}{y≥x-1}\\{y≥1-x}\\{y≤1}\end{array}\right.$,则p是q的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
6.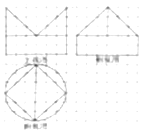 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )| A. | 9+16π | B. | 9+18π | C. | 12+18π | D. | 18+18π |
20.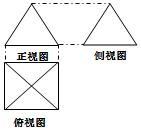 如果一个几何体的三视图如图所示,正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形,(单位长度:cm),则此几何体的侧面积是( )
如果一个几何体的三视图如图所示,正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形,(单位长度:cm),则此几何体的侧面积是( )
 如果一个几何体的三视图如图所示,正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形,(单位长度:cm),则此几何体的侧面积是( )
如果一个几何体的三视图如图所示,正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形,(单位长度:cm),则此几何体的侧面积是( )| A. | .$2\sqrt{3}$cm | B. | .$4\sqrt{3}$cm2 | C. | 8 cm2 | D. | 12 cm2 |
5.中心在坐标原点的双曲线C的两条渐近线与圆(x-2)2+y2=3相切,则双曲线的离心率为( )
| A. | 2 | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2或$\frac{2\sqrt{3}}{3}$ |
