题目内容
4.已知不等式|x+3|-2x-1<0的解集为(x0,+∞)(Ⅰ)求x0的值;
(Ⅱ)若函数f(x)=|x-m|+|x+$\frac{1}{m}$|-x0(m>0)有零点,求实数m的值.
分析 (Ⅰ)不等式转化为$\left\{\begin{array}{l}{x≤-3}\\{-(x+3)-2x-1<0}\end{array}\right.$或$\left\{\begin{array}{l}{x>-3}\\{x+3-2x-1<0}\end{array}\right.$,解得x>2,即可求x0的值;
(Ⅱ)由题意,等价于|x-m|+|x+$\frac{1}{m}$|=2(m>0)有解,结合基本不等式,即可求实数m的值.
解答 解:(Ⅰ)不等式转化为$\left\{\begin{array}{l}{x≤-3}\\{-(x+3)-2x-1<0}\end{array}\right.$或$\left\{\begin{array}{l}{x>-3}\\{x+3-2x-1<0}\end{array}\right.$,
解得x>2,∴x0=2;
(Ⅱ)由题意,等价于|x-m|+|x+$\frac{1}{m}$|=2(m>0)有解,
∵|x-m|+|x+$\frac{1}{m}$|≥m+$\frac{1}{m}$,当且仅当(x-m)(x+$\frac{1}{m}$)≤0时取等号,
∵|x-m|+|x+$\frac{1}{m}$|=2(m>0)有解,
∴m+$\frac{1}{m}$≤2,
∵m+$\frac{1}{m}$≥2,
∴m+$\frac{1}{m}$=2,∴m=1.
点评 本题考查不等式的解法,考查绝对值不等式,考查基本不等式的运用,属于中档题.

练习册系列答案
相关题目
14.从5名男同学,4名女同学中任选5人参加一次夏令营,其中男同学,女同学均不少于2人的概率是( )
| A. | $\frac{13}{63}$ | B. | $\frac{50}{63}$ | C. | $\frac{43}{63}$ | D. | $\frac{11}{63}$ |
14.过点A(3,5)作圆(x-2)2+(y-3)2=1的切线,则切线的方程为( )
| A. | x=3或3x+4y-29=0 | B. | y=3或3x+4y-29=0 | C. | x=3或3x-4y+11=0 | D. | y=3或3x-4y+11=0 |
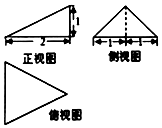 已知某三棱锥的三视图如图所示,则该三棱锥的体积为$\frac{2}{3}$,它的表面积为$2+2\sqrt{5}$.
已知某三棱锥的三视图如图所示,则该三棱锥的体积为$\frac{2}{3}$,它的表面积为$2+2\sqrt{5}$.