题目内容
对于n∈N*,将n表示为n=a0×2k+a1×2k-1+a2×2k-2+…+ak-1×21+ak×20,当i=0时,ai=1,当1≤i≤k时,ai为0或1,记I(n)为上述表示中ai为0的个数,例如:1=1×20,4=1×22+0×21+0×20,故I(1)=0,Ⅰ(4)=2,则:
(1)Ⅰ(12)= ;
(2)
I(n)= .
(1)Ⅰ(12)=
(2)
| 63 |
 |
| n=1 |
考点:进行简单的合情推理
专题:规律型
分析:(1)根据题意,分析可得,将n 表示n=a0×2k+a1×2k-1+a2×2k-2+…+ak-1×21+ak×20,实际是将十进制的数转化为二进制的数,易得12=1×23+1×22+0×21+0×20,由I(n)的意义,可得答案;
(2)将n分为n=127,64≤n≤126,32≤n≤63,…n=1等7种情况,有组合数的性质,分析其中I(n)的取值情况,与二项式定理结合,可转化为等比数列的前7项和,计算可得答案.
(2)将n分为n=127,64≤n≤126,32≤n≤63,…n=1等7种情况,有组合数的性质,分析其中I(n)的取值情况,与二项式定理结合,可转化为等比数列的前7项和,计算可得答案.
解答:
解:(1)根据题意,12=1×23+1×22+0×21+0×20,则I(12)=2;
(2)63=1×25+1×24+1×23+1×22+1×21+1×20,
设32≤n≤63,且n为整数;
则n=1×25+a1×24+a2×23+a3×22+a4×21+a5×20,
a1,a2,a3,a4,a5中6个数都为0或1,
其中没有一个为1时,有C50种情况,即有C50个I(n)=5;
其中有一个为1时,有C51种情况,即有C51个I(n)=4;
其中有2个为1时,有C52种情况,即有C52个I(n)=3;
…
I(n)=C50×5+C51×4+C52×3+C53×2+C54×1+C55×0=80,
同理可得:
I(n)=32,
I(n)=12,
I(n)=4,
I(n)=1,I(1)=0,
∴
I(n)=
I(n)+
I(n)+
I(n)+
I(n)+
I(n)+I(1)=80+32+12+4+1+0=129;
故答案为:(1)2;(2)129
(2)63=1×25+1×24+1×23+1×22+1×21+1×20,
设32≤n≤63,且n为整数;
则n=1×25+a1×24+a2×23+a3×22+a4×21+a5×20,
a1,a2,a3,a4,a5中6个数都为0或1,
其中没有一个为1时,有C50种情况,即有C50个I(n)=5;
其中有一个为1时,有C51种情况,即有C51个I(n)=4;
其中有2个为1时,有C52种情况,即有C52个I(n)=3;
…
| 63 |
 |
| n=32 |
同理可得:
| 31 |
 |
| n=16 |
| 15 |
 |
| n=8 |
| 7 |
 |
| n=4 |
| 3 |
 |
| n=2 |
∴
| 63 |
 |
| n=1 |
| 63 |
 |
| n=32 |
| 31 |
 |
| n=16 |
| 15 |
 |
| n=8 |
| 7 |
 |
| n=4 |
| 3 |
 |
| n=2 |
故答案为:(1)2;(2)129
点评:解本题关键在于分析题意,透彻理解I(n)的含义及
I(n)的运算,注意转化思想,结合二项式定理与等比数列的前n项和公式进行计算.
| 63 |
 |
| n=1 |

练习册系列答案
相关题目
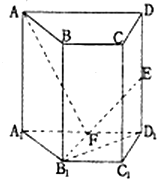 如图,四棱柱ABCD-A1B1C1D1中,侧棱DD1⊥底面ABCD,AD⊥DC,AD∥BC,AD=DD1=2,BC=DC=1.点E是侧棱DD1的中点.
如图,四棱柱ABCD-A1B1C1D1中,侧棱DD1⊥底面ABCD,AD⊥DC,AD∥BC,AD=DD1=2,BC=DC=1.点E是侧棱DD1的中点.