题目内容
设θ为两个非零向量
，
的夹角，已知对任意实数t，|
-t
|的最小值是2，则（ ）
| a |
| b |
| b |
| a |
A、若θ确定，则|
| ||
B、若θ确定，则|
| ||
C、若|
| ||
D、若|
|
考点：数量积表示两个向量的夹角
专题：平面向量及应用
分析：由题意可得 |
-t•
|2=
2•t2-2
•
•t+
2，它是关于变量t的一个二次函数，再利用二次函数的性质可得结论．
| b |
| a |
| a |
| a |
| b |
| b |
解答：
解：由题意可得 |
-t•
|2=
2•t2-2
•
•t+
2，它是关于变量t的一个二次函数，
故当t=
=
=
cosθ （其中，θ为
、
的夹角），
|
-t
|取得最小值2，
即|
|2sin2θ=2，
故当θ唯一确定时，|
|唯一确定，
故选：B．
| b |
| a |
| a |
| a |
| b |
| b |
故当t=
| ||||
|
|
| ||||
|
|
|
| ||
|
|
| a |
| b |
|
| b |
| a |
即|
| b |
故当θ唯一确定时，|
| b |
故选：B．
点评：本题主要考查两个向量的夹角公式的应用，求向量的模的方法，属于基础题．
练习册系列答案
智能训练练测考系列答案
相关题目
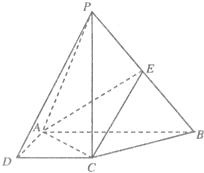如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，AB⊥AD，AB∥CD，AB=2AD=2CD=2，BC=与向量
=（1，2，3），
=（3，1，2）都垂直的向量为（ ）
| a |
| b |
| A、（1，7，5） |
| B、（1，-7，5） |
| C、（-1，-7，5） |
| D、（1，-7，-5） |