题目内容
化简:
+
.
| |sinx| |
| sinx |
| cosx |
| |cosx| |
考点:三角函数的化简求值
专题:三角函数的求值
分析:由条件结合三角三角函数在各个象限中的符号,分类讨论求得它的值.
解答:
解:若x为第一象限角,则
+
=
+
=2;
若x为第二象限角,则
+
=
-
=0;
若x为第三象限角,则
+
=-
-
=-2;
若x为第四象限角,则
+
=-
+
=0.
综上可得,当x为第一象限角时,要求式子的值为2;
当x为第三象限角时,要求式子的值为-2;
当x为第二、四象限角时,要求式子的值为0.
| |sinx| |
| sinx |
| cosx |
| |cosx| |
| sinx |
| sinx |
| cosx |
| cosx |
若x为第二象限角,则
| |sinx| |
| sinx |
| cosx |
| |cosx| |
| sinx |
| sinx |
| cosx |
| cosx |
若x为第三象限角,则
| |sinx| |
| sinx |
| cosx |
| |cosx| |
| sinx |
| sinx |
| cosx |
| cosx |
若x为第四象限角,则
| |sinx| |
| sinx |
| cosx |
| |cosx| |
| sinx |
| sinx |
| cosx |
| cosx |
综上可得,当x为第一象限角时,要求式子的值为2;
当x为第三象限角时,要求式子的值为-2;
当x为第二、四象限角时,要求式子的值为0.
点评:本题主要考查三角三角函数在各个象限中的符号,体现了分类讨论的数学额思想,属于基础题.

练习册系列答案
相关题目
下列命题正确的是( )
| A、?x∈R,都有x2-3x+3>0成立 |
| B、?x0∈R,使sin2x0+cos2x0<1成立 |
| C、“?x0∈R,使x02-1<0”的否定是“?x∈R,都有x2-1>0” |
| D、若“p∨q”为假,则命题p、q中一个真另一个假 |
如图所示的程序框图输出的结果是S=14,则判断框内应填的条件是( )


| A、i≥7? | B、i>15? |
| C、i≥15? | D、i>31? |
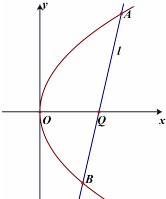 已知抛物线G:y2=2px(p>0)的焦点到准线的距离为2,过点Q(a,0)(a>0)的直线l交抛物线G于A,B两点(如图所示).
已知抛物线G:y2=2px(p>0)的焦点到准线的距离为2,过点Q(a,0)(a>0)的直线l交抛物线G于A,B两点(如图所示).