题目内容
16.综合应用抛物线和双曲线的光学性质,可以设计制造反射式天文望远镜.这种望远镜的特点是,镜筒可以很短而观察天体运动又很清楚,例如,某天文仪器厂设计制造的一种反射式望远镜,其光学系统的原理如图1(中心截口示意图)所示,其中,一个反射镜PO1Q弧所在的曲线为抛物线,另一个反射镜MO2N弧所在的曲线为双曲线的一个分支,已知F1、F2是双曲线的两个焦点,其中F2同时又是抛物线的焦点,O1也是双曲线的左顶点.若在如图2所示的坐标系下,MO2N弧所在的曲线方程为标准方程,试根据图示尺寸(单位:cm),写出反射镜PO1Q弧所在的抛物线方程为y2=920(x+88).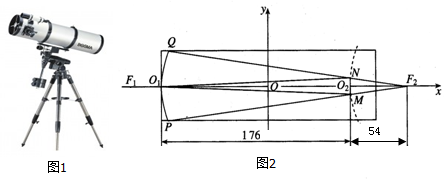
分析 根据题意,对于双曲线,有$\left\{\begin{array}{l}{c-a=54}\\{2a=176}\end{array}\right.$,求出a,b,c可得双曲线的方程;求出抛物线的顶点的横坐标,可得抛物线的方程.
解答 解:对于双曲线,有$\left\{\begin{array}{l}{c-a=54}\\{2a=176}\end{array}\right.$,∴a=88,c=142,
由题意,$\frac{p}{2}$=142+88=230
∵抛物线的顶点的横坐标是-88,
∴抛物线的方程为y2=920(x+88).
故答案为y2=920(x+88).
点评 本题考查利用数学知识解决实际问题,考查双曲线、抛物线的性质,属于中档题.

练习册系列答案
相关题目
6.已知函数f(x)=(x3+2x2+ax-a)ex,f′(x)为f(x)的导函数,则f′(0)的值为( )
| A. | 0 | B. | 1 | C. | -a | D. | 不确定 |
11.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线与抛物线$y=\frac{1}{2}{x^2}+\frac{1}{2}$只有一个公共点,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | 5 | C. | 2 | D. | $\sqrt{5}$ |
8.已知椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1以及椭圆内一点P(2,1),则以P为中点的弦所在直线斜率为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
5.若复数z满足z(4-i)=5+3i(i为虚数单位),则复数z的共轭复数为( )
| A. | 1-i | B. | -1+i | C. | 1+i | D. | -1-i |