题目内容
12.阅读材料:根据两角和与差的正弦公式,有:sin(α+β)=sinαcosβ+cosαsinβ------①
sin(α-β)=sinαcosβ-cosαsinβ------②
由①+②得sin(α+β)+sin(α-β)=2sinαcosβ------③
令α+β=A,α-β=β 有α=$\frac{A+B}{2}$,β=$\frac{A-B}{2}$代入③得 sinA+sinB=2sin$\frac{A+B}{2}$cos$\frac{A-B}{2}$.
(1)利用上述结论,试求sin15°+sin75°的值;
(2)类比上述推证方法,根据两角和与差的余弦公式,证明:cosA-cosB=-2sin$\frac{A+B}{2}$cos$\frac{A-B}{2}$.
分析 (1)令A=15°,B=75°,代和可得sin15°+sin75°的值;
(2)由cos(α+β)=cosαcosβ-sinαsinβ,cos(α-β)=cosαcosβ+sinαsinβ两式相加得:cos(α+β)+cos(α-β)=2cosαcosβ,令α+β=A,α-β=B 有α=$\frac{A+B}{2}$,β=$\frac{A-B}{2}$,可得结论;
解答 解:(1)∵sinA+sinB=2sin$\frac{A+B}{2}$cos$\frac{A-B}{2}$,
∴sin15°+cos75°=2sin$\frac{15°+75°}{2}$cos$\frac{15°-75°}{2}$,
=2sin45°•cos(-30°)=$\frac{\sqrt{6}}{2}$,
∴sin15°+cos75°=$\frac{\sqrt{6}}{2}$,
(2)证明:因为cos(α+β)=cosαcosβ-sinαsinβ,------①
cos(α-β)=cosαcosβ+sinαsinβ------②
①+②得cos(α+β)+cos(α-β)=2cosαcosβ,③
令α+β=A,α-β=B 有α=$\frac{15°+75°}{2}$,β=$\frac{15°-75°}{2}$,
代入③得:cosA-cosB=-2sin$\frac{A+B}{2}$cos$\frac{A-B}{2}$.
∴cosA-cosB=-2sin$\frac{A+B}{2}$cos$\frac{A-B}{2}$.
点评 本题主要考查两角和与差三角函数公式、二倍角公式、三角函数的恒等变换等基础知识,考查推理论证能力,运算求解能力,考查化归与转化思想等,属于中档题.

练习册系列答案
相关题目
3.已知;$f(n)=\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}$,则f(n+1)-f(n)=( )
| A. | $\frac{1}{2n+1}+\frac{1}{2n+2}$ | B. | $\frac{1}{2n+2}-\frac{1}{n+1}$ | ||
| C. | $\frac{1}{2n+2}$ | D. | $\frac{1}{2n+1}+\frac{1}{2n+2}-\frac{1}{n+1}$ |
20.下列说法正确的是( )
| A. | 类比推理、归纳推理、演绎推理都是合情推理 | |
| B. | 合情推理得到的结论一定是正确的 | |
| C. | 合情推理得到的结论不一定正确 | |
| D. | 归纳推理得到的结论一定是正确的 |
17.下列有关于f(x)=ln(1+|x|)-$\frac{1}{1{+x}^{2}}$的性质的描述,正确的是( )
| A. | 奇函数,在R上单调递增 | |
| B. | 奇函数,在(-∞,0)上单调递增,在(0,+∞)上单调递增 | |
| C. | 偶函数,在(-∞,0)上单调递减,在(0,+∞)上单调递增 | |
| D. | 偶函数,在(-∞,0)上单调递增,在(0,+∞)上单调递减 |
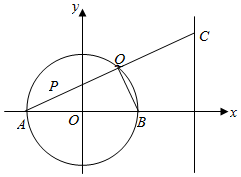 已知圆O:x2+y2=9,直线l1:x=6,圆O与x轴相交于点A,B(如图),点P(-1,2)是圆O内一点,点Q为圆O上任一点(异于点A、B),直线AQ与l1相交于点C.
已知圆O:x2+y2=9,直线l1:x=6,圆O与x轴相交于点A,B(如图),点P(-1,2)是圆O内一点,点Q为圆O上任一点(异于点A、B),直线AQ与l1相交于点C.