题目内容
已知a>0且a≠1,f(logax)=
(x-
).
(1)求f(x);
(2)讨论f(x)的单调性和奇偶性;
(3)若f(x)定义域为(-1,1),解不等式f(1-m)+f(1-m2)<0.
| a |
| a2-1 |
| 1 |
| x |
(1)求f(x);
(2)讨论f(x)的单调性和奇偶性;
(3)若f(x)定义域为(-1,1),解不等式f(1-m)+f(1-m2)<0.
考点:奇偶性与单调性的综合,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)利用换元法,即可求f(x)的解析式;
(2)根据函数奇偶性和单调性的定义即可证明f(x)的奇偶性与单调性;
(3)根据函数奇偶性和单调性的性质将不等式f(1-m)+f(1-m2)<0进行转化,求m的取值范围.
(2)根据函数奇偶性和单调性的定义即可证明f(x)的奇偶性与单调性;
(3)根据函数奇偶性和单调性的性质将不等式f(1-m)+f(1-m2)<0进行转化,求m的取值范围.
解答:
解:(1)令t=logax(t∈R)
则x=at,f(t)=
(at-a-t),
∴f(x)=
(ax-a-x)(x∈R),
(2)∵x∈R,f(-x)=
(a-x-ax)=-
(ax-a-x)=-f(x),
∴函数f(x)为奇函数.
设x1<x2,
若a>1,f(x2)-f(x1)=
[ax2-a-x2-ax1+a-x1]=
[(ax2-ax1)(1+
)],
∵a>1,x1<x2,∴ax1<ax2,ax2-ax1>0,ax1ax2>0,
>0,
∴f(x2)-f(x1)>0,即f(x2)>f(x1),
类似可证明当0<a<1时,f(x2)>f(x1),
综上,无论a>1或0<a<1,f(x)在R上都是增函数.
(3)不等式f(1-m)+f(1-m2)<0化为f(1-m)<-f(1-m2)=f(m2-1)
即f(1-m)<f(m2-1),
∵f(x)定义域为(-1,1),且函数为增函数,
∴
,
即
,
则
,
解得1<m<
.
则x=at,f(t)=
| a |
| a2-1 |
∴f(x)=
| a |
| a2-1 |
(2)∵x∈R,f(-x)=
| a |
| a2-1 |
| a |
| a2 -1 |
∴函数f(x)为奇函数.
设x1<x2,
若a>1,f(x2)-f(x1)=
| a |
| a2-1 |
| a |
| a2-1 |
| 1 |
| ax1ax2 |
∵a>1,x1<x2,∴ax1<ax2,ax2-ax1>0,ax1ax2>0,
| a |
| a2-1 |
∴f(x2)-f(x1)>0,即f(x2)>f(x1),
类似可证明当0<a<1时,f(x2)>f(x1),
综上,无论a>1或0<a<1,f(x)在R上都是增函数.
(3)不等式f(1-m)+f(1-m2)<0化为f(1-m)<-f(1-m2)=f(m2-1)
即f(1-m)<f(m2-1),
∵f(x)定义域为(-1,1),且函数为增函数,
∴
|
即
|
则
|
解得1<m<
| 2 |
点评:本题主要考查函数奇偶性和单调性的判断以及不等式恒成立的证明,根据函数奇偶性和单调性的定义是解决本题的关键.

练习册系列答案
相关题目
从点P(1,-2)引圆(x+1)2+(y-1)2=4的切线,则切线长是( )
| A、4 | B、3 | C、2 | D、1 |
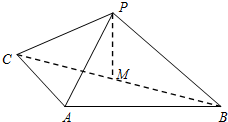 如图,△PAB是边长为2的正三角形,平面PAB外一动点C满足下面条件:PC=PA,AC⊥AB.
如图,△PAB是边长为2的正三角形,平面PAB外一动点C满足下面条件:PC=PA,AC⊥AB.