题目内容
已知an=an(a是常数,a≠0且a≠1),Sn为|an|的前n项和,bn=
+1,若数列|bn|是等比数列,则a= .
| 2Sn |
| an |
考点:数列的求和
专题:等差数列与等比数列
分析:依题意,通过对参数a分a>0与a<0两类讨论,可分别求得b1、b1、b1的值,利用数列|bn|是等比数列,得|b2|2=|b1|•|b3|,从而可求得a的值.
解答:
解:∵bn=
+1,an=an(a是常数,a≠0且a≠1),
当a>0时,|bn|=bn,
∴b1=
+1=
+1=3,
b2=
+1=
+1=
+3,
b3=
+1=
+
+3,
∵数列|bn|是等比数列,
∴|b2|2=|b1|•|b3|,即b22=b1•b3,(
+3)2=3(
+
+3),
整理得:
-
=0,解得a=
.
当a<0时,同理可得b1=-1,b2=-
+3,b3=-
+
-1,
∵数列|bn|是等比数列,
∴(-
+3)2=1×(
-
+1),
整理得:
-
+4=0,解得
=1(舍去)或
=4(舍去).
综上所述,a=
.
故答案为:
.
| 2Sn |
| an |
当a>0时,|bn|=bn,
∴b1=
| 2|a1| |
| a1 |
| 2|a| |
| a |
b2=
| 2(|a1|+|a2|) |
| a2 |
| 2(a+a2) |
| a2 |
| 2 |
| a |
b3=
| 2(a+a2+a3) |
| a3 |
| 2 |
| a2 |
| 2 |
| a |
∵数列|bn|是等比数列,
∴|b2|2=|b1|•|b3|,即b22=b1•b3,(
| 2 |
| a |
| 2 |
| a2 |
| 2 |
| a |
整理得:
| 1 |
| a2 |
| 3 |
| a |
| 1 |
| 3 |
当a<0时,同理可得b1=-1,b2=-
| 2 |
| a |
| 2 |
| a2 |
| 2 |
| a |
∵数列|bn|是等比数列,
∴(-
| 2 |
| a |
| 2 |
| a2 |
| 2 |
| a |
整理得:
| 1 |
| a2 |
| 5 |
| a |
| 1 |
| a |
| 1 |
| a |
综上所述,a=
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查递推关系的应用,突出考查等比关系的确定,考查分类讨论思想与综合运算能力,属于难题.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目

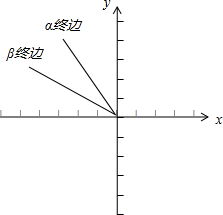 已知α是第二象限角,在第二象限内将角α的终边绕原点按逆时针方向旋转,得到第二象限角β的终边,如图所示,利用单位圆中的三角函数线比较下列各组数的大小.
已知α是第二象限角,在第二象限内将角α的终边绕原点按逆时针方向旋转,得到第二象限角β的终边,如图所示,利用单位圆中的三角函数线比较下列各组数的大小.