已知四棱锥P-ABCD中.底面四边形ABCD为等腰梯形.且AB∥CD.AB=$\frac{1}{2}$CD.PA=PB=AD.PA+AD=CD=4$\sqrt{3}$.若平面PAB⊥平面ABCD.则四棱锥P-ABCD外接球的表面积为52π．题目和参考答案——青夏教育精英家教网—

题目内容

2．

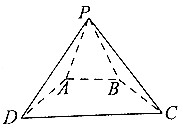已知四棱锥P-ABCD中，底面四边形ABCD为等腰梯形，且AB∥CD，AB=$\frac{1}{2}$CD，PA=PB=AD，PA+AD=CD=4$\sqrt{3}$，若平面PAB⊥平面ABCD，则四棱锥P-ABCD外接球的表面积为52π．

分析作出图形，确定球心的位置，利用勾股定理建立方程，即可得出结论．

解答解：由题意，PA=AD=2$\sqrt{3}$，PF=FG=3，球心O在平面ABCD中的射影为CD的中点，如图所示，
设OG=d，则$9+（3-d）^{2}={d}^{2}+（2\sqrt{3}）^{2}$，
∴d=1，$r=\sqrt{13}$，
∴四棱锥P-ABCD外接球的表面积为4π•13=52π，
故答案为52π．

点评本题考查四棱锥P-ABCD外接球的表面积，考查学生的计算能力，确定球心位置，求出球的半径是关键．

练习册系列答案

16．已知函数f（x）=|x-a|-$\frac{1}{2}$x，（a＞0）．
（Ⅰ）若a=3，解关于x的不等式f（x）＜0；
（Ⅱ）若对于任意的实数x，不等式f（x）-f（x+a）＜a²+$\frac{a}{2}$恒成立，求实数a的取值范围．

13．已知p：-x²+7x+8≥0，q：x²-2x+1-4m²≤0．若“￢p”是“￢q”的充分不必要条件，则实数m的取值范围为[-1，1]．

20．对于函数f₁（x），f₂（x），h（x），如果存在实数a，b使得h（x）=a•f₁（x）+b•f₂（x），那么称h（x）为f₁（x），f₂（x）的生成函数．
（1）给出函数${f_1}（x）=lg\frac{x}{10}，\;\;{f_2}（x）=lg10x，\;\;h（x）=lgx$，h（x）是否为f₁（x），f₂（x）的生成函数？并说明理由；
（2）设${f_1}（x）={log_2}x，\;\;{f_2}（x）={log_{\frac{1}{2}}}x，\;\;a=2，\;\;b=1$，生成函数h（x）．若不等式3h²（x）+2h（x）+t＞0在x∈[2，4]上恒成立，求实数t的取值范围；
（3）设${f_1}（x）=x\;\;（x＞0），\;\;\;{f_2}（x）=\frac{1}{x}\;\;\;（x＞0）$，取a＞0，b＞0，生成函数h（x）图象的最低点坐标为（2，8）．若对于任意正实数x₁，x₂且x₁+x₂=1．试问是否存在最大的常数m，使h（x₁）h（x₂）≥m恒成立？如果存在，求出这个m的值；如果不存在，请说明理由．

7．求函数y=3${\;}^{-{x}^{2}+2x+3}$的值域和单调区间．

14．

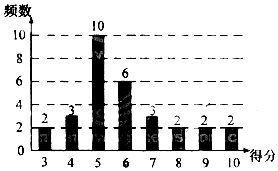为了普及环保知识，增强环保意识，某大学随即抽取30名学生参加环保知识测试，得分（十分制）如图所示，假设得分值的中位数为m，众数为n，平均值为$\overline{x}$，则（　　）

11．已知m，n是两条不同直线α，β是两个不同平面，则下列命题正确的是（　　）

	A．	若α，β垂直于同一平面，则α与β平行
	B．	若m，n平行于同一平面，则m与n平行
	C．	若m，n不平行，则m与n不可能垂直于同一平面
	D．	若α，β不平行，则在α内不存在与β平行的直线

12．已知函数$f（x）=\frac{3-a}{{{a^x}+1}}+asinx$，那么下列命题正确的是（　　）

	A．	若a=0，则y=f（x）与y=3是同一函数
	B．	若0＜a≤1，则$f（-\frac{π}{2}）＜f（2-{log_3}2）＜f[{（\frac{1}{3}）^{{{log}_3}\frac{2}{3}}}]＜f（{log_3}5）＜f（\frac{π}{2}）$
	C．	若a=2，则对任意使得f（m）=0的实数m，都有f（-m）=1
	D．	若a＞3，则f（cos2）＜f（cos3）

试题分类