题目内容
求椭圆
+
=1的长轴长、短轴长、焦点坐标、顶点坐标及离心率,并用描点法画出该椭圆的图形.
| x2 |
| 9 |
| y2 |
| 4 |
考点:椭圆的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:分别求出椭圆的a,b,c,运用椭圆的性质,即可得到长轴长、短轴长、焦点坐标、顶点坐标及离心率;再列表描点画图:首先列表,再根据表中的x、y对应坐标值,描点,画出椭圆的图象.
解答:
解:椭圆
+
=1的a=3,b=2,c=
=
,
则长轴长为2a=6,短轴长为2b=4,焦点坐标为(-
,0),(
,0),
顶点坐标为(-3,0),(3,0),(0,-2),(0,2),离心率e=
=
.
列表:
描点连线,得到如图:
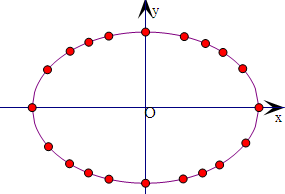
| x2 |
| 9 |
| y2 |
| 4 |
| 9-4 |
| 5 |
则长轴长为2a=6,短轴长为2b=4,焦点坐标为(-
| 5 |
| 5 |
顶点坐标为(-3,0),(3,0),(0,-2),(0,2),离心率e=
| c |
| a |
| ||
| 3 |
列表:
| x | 0 | ±
| ±1 | ±
| ±2 | ±
| ±3 | ||||||||||||||||||
| y | ±2 | ±
| ±
| ±
| ±
| ±
| 0 |

点评:本题考查椭圆的方程和性质,及椭圆的图形,考查运算能力,作图能力,属于基础题.

练习册系列答案
相关题目
下面两个程序最后输出的“sum”应分别等于( )


| A、都是17 | B、都是21 |
| C、21和17 | D、14和21 |
已知a,b,c是正实数,则“
b=a+2c”是“b2≥4ac”的( )
| 2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
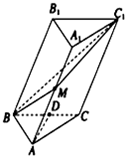 如图所示,在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.
如图所示,在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.