题目内容
已知a,b,c是正实数,则“
b=a+2c”是“b2≥4ac”的( )
| 2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:分为充分性和必要性推导,利用基本不等式求解.
解答:
解:充分性:∵a>0,c>0,∴a+2c≥2
,
又∵
b=a+2c,∴
b≥2
,
∴b≥2
,∴b2≥4ac,即充分性成立;
必要性:b=2,a=c=1时,4≥4成立,但不满足
b=a+2c,必要性不成立;
故“
b=a+2c”是“b2≥4ac”的充分而不必要条件,
故选:A.
| 2ac |
又∵
| 2 |
| 2 |
| 2ac |
∴b≥2
| ac |
必要性:b=2,a=c=1时,4≥4成立,但不满足
| 2 |
故“
| 2 |
故选:A.
点评:本题考查充要条件,注意利用基本不等式求解,必要性不成立使用特值否定.

练习册系列答案
相关题目
方程log
x=2x-2014的实数根的个数为( )
| 1 |
| 2 |
| A、0 | B、1 | C、2 | D、不确定 |
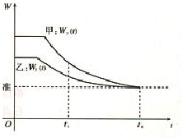 国家环保总局对长期超标准排放污物,污染严重而又未进行治理的单位,规定出一定期限,强令在此期限内完成排污治理.如图是国家环保总局在规定的排污达标日期前,对甲、乙两家企业连续检测的结果(W表示排污量),哪个企业治理的效率比较高?为什么?
国家环保总局对长期超标准排放污物,污染严重而又未进行治理的单位,规定出一定期限,强令在此期限内完成排污治理.如图是国家环保总局在规定的排污达标日期前,对甲、乙两家企业连续检测的结果(W表示排污量),哪个企业治理的效率比较高?为什么?