题目内容
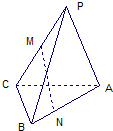 如图P是△ABC所在平面外一点,PA=PB,CB⊥平面PAB,M是PC的中点,N是AB上的点,AN=3NB.求证:MN⊥AB.
如图P是△ABC所在平面外一点,PA=PB,CB⊥平面PAB,M是PC的中点,N是AB上的点,AN=3NB.求证:MN⊥AB.考点:直线与平面垂直的性质
专题:空间位置关系与距离
分析:取AB中点Q,连接PQ,CQ,由线面垂直得PQ⊥BC,由等腰三角形性质得PQ⊥AB,由∠CBP=90°,MB=
PC,N是BQ的中点,由此能证明MN⊥AB.
| 1 |
| 2 |
解答:
证明:取AB中点Q,连接PQ,CQ,
因为CB⊥平面PAB,
则PQ⊥BC,又PA=PB,所以PQ⊥AB,
于是PQ⊥平面ABC,所以∠PQC=90°,
因为M是PC中点,所以MQ=
PC,
又因为∠CBP=90°,所以MB=
PC,所以MB=MQ;
而N是BQ的中点,所以MN⊥AB.

因为CB⊥平面PAB,
则PQ⊥BC,又PA=PB,所以PQ⊥AB,
于是PQ⊥平面ABC,所以∠PQC=90°,
因为M是PC中点,所以MQ=
| 1 |
| 2 |
又因为∠CBP=90°,所以MB=
| 1 |
| 2 |
而N是BQ的中点,所以MN⊥AB.
点评:本题考查异面直线的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 已知圆C:(x-1)2+(y-1)2=2经过椭圆Γ:
已知圆C:(x-1)2+(y-1)2=2经过椭圆Γ:
 如图,已知⊙O的直径AB=3,点C为⊙O上异于A,B的一点,VC⊥平面ABC,且VC=2,点M为线段VB的中点.
如图,已知⊙O的直径AB=3,点C为⊙O上异于A,B的一点,VC⊥平面ABC,且VC=2,点M为线段VB的中点.